2  Data visualization

For more information

Expansion Pack in the Open World:

官方Portal

https://ggplot2.tidyverse.org/index.html

2.1 Introduction

“The simple graph has brought more information to the data analyst’s mind than any other device.” — John Tukey

「对数据分析者来说，简单的画图传递的信息，比其他方式都要多。」— John Tukey

从本页面你会学到什么？

目标 Objective: 面对一个问题，迅速判断出一个什么样的图可以回答该问题，迅速用ggplot2的语法实现。

实现途径：通过使用 ggplot 分析 palmerpenguins 包下的 penguins 数据集，感受，熟悉 ggplot2 的语法逻辑。

2.1.0.0.1 阅读本章后，你可以做到的几件事：

1. 看类似如下代码时，感到简单和亲切，脑子里已经有画面了。

ggplot(
  data = dataset, 
  mapping = aes(x = x_var, y = y_var)
) +
  geom_point(mapping = aes(color = cat_var)) +
  geom_smmoth(method = "lm") +
  labs(
  title = "X and Y",
    subtitle = "Dimensions for Cat1, Cat2 and Cat3",
    x = "X of interst", y = " Y of interest"
) +
 scale_color_colorblind()

R has several systems for making graphs, but ggplot2 is one of the most elegant and most versatile. ggplot2 implements the grammar of graphics, a coherent system for describing and building graphs. With ggplot2, you can do more and faster by learning one system and applying it in many places.

• ggplot2 执行一种画图语法。学 习一种系统，逻辑，用到很多地方

This chapter will teach you how to visualize your data using ggplot2. We will start by creating a simple scatterplot and use that to introduce aesthetic mappings and geometric objects – the fundamental building blocks of ggplot2.

这一章，将通过介绍如何使用 ggplot2 绘制散点图，介绍 aesthetic mappings (mapping, aes()), and geometric objects (geom_).

2.2 准备工作

注意：为了获取企鹅数据，满足具体的可视化需求，本章的代码「额外」加载了palmerpenguins, ggthemes这两个包。

说「额外」，是因为有两个包是默认需要一直处在加载状态下的：数据科学的核心R包 tidyverse，以及核心画图包ggplot2。

【新手武器】也就是说，为了完成这一章主要的数据可视化项目，你需要安装/下载 (install.packages / 从panel上点install按钮并搜索) 并载入 (library) 至少4个包。解决如同时展示多个图的功能有可能需要其它的包。有 需要时，我们随时安装，加载即可。

This chapter focuses on ggplot2, one of the core packages in the tidyverse. To access the datasets, help pages, and functions used in this chapter, load the tidyverse by running:

library(tidyverse) # 这里为了使用函数 glimpse
#> ── Attaching core tidyverse packages ───────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr     1.1.4     ✔ readr     2.1.5
#> ✔ forcats   1.0.0     ✔ stringr   1.5.1
#> ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
#> ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
#> ✔ purrr     1.0.2     
#> ── Conflicts ─────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag()    masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(ggplot2)

In addition to tidyverse, we will also use the palmerpenguins package, which includes the penguins dataset containing body measurements for penguins on three islands in the Palmer Archipelago, and the ggthemes package, which offers a colorblind safe color palette.

palmerpenguins：数据 penguins需要加载此包进行获取。

ggthemes： 对色盲人士友好的配色方案。

library(palmerpenguins)
library(ggthemes)

You only need to install a package once, but you need to load it every time you start a new session.

【新手武器】对于R包，你只需要安装一次，但每一次start a new session(比如，开启新的project) 都需要加载

数据迅速探索：moderndive, autoReg

library(moderndive)
library(skimr)

library(autoReg)

2.3 最被忽略的往往是最重要的事情

你想回答什么问题？

提出你的问题：0th iteration

Do penguins with longer flippers weigh more or less than penguins with shorter flippers? You probably already have an answer, but try to make your answer precise.

What does the relationship between flipper length and body mass look like? Is it positive? Negative? Linear? Nonlinear? Does the relationship vary by the species of the penguin? How about by the island where the penguin lives? Let’s create visualizations that we can use to answer these questions.

2.3.1 「企鹅」数据框： The penguins data frame

2.3.2 策略：瞥(glimpse)你的数据

penguins
#> # A tibble: 344 × 8
#>   species island    bill_length_mm bill_depth_mm flipper_length_mm
#>   <fct>   <fct>              <dbl>         <dbl>             <int>
#> 1 Adelie  Torgersen           39.1          18.7               181
#> 2 Adelie  Torgersen           39.5          17.4               186
#> 3 Adelie  Torgersen           40.3          18                 195
#> 4 Adelie  Torgersen           NA            NA                  NA
#> 5 Adelie  Torgersen           36.7          19.3               193
#> 6 Adelie  Torgersen           39.3          20.6               190
#> # ℹ 338 more rows
#> # ℹ 3 more variables: body_mass_g <int>, sex <fct>, year <int>

迅速鸟瞰数据集：1. glimpse()

For an alternative view, where you can see all variables and the first few observations of each variable, use glimpse(). Or, if you’re in RStudio, run View(penguins) to open an interactive data viewer.

glimpse(penguins)
#> Rows: 344
#> Columns: 8
#> $ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, A…
#> $ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torge…
#> $ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.…
#> $ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.…
#> $ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, …
#> $ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 347…
#> $ sex               <fct> male, female, female, NA, female, male, female, m…
#> $ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2…

#View(penguins) 

comment this out. Quarto runs into presenting issue regarding View().

Base R 函数: 原先

summary(penguins)
#>       species          island    bill_length_mm  bill_depth_mm  
#>  Adelie   :152   Biscoe   :168   Min.   :32.10   Min.   :13.10  
#>  Chinstrap: 68   Dream    :124   1st Qu.:39.23   1st Qu.:15.60  
#>  Gentoo   :124   Torgersen: 52   Median :44.45   Median :17.30  
#>                                  Mean   :43.92   Mean   :17.15  
#>                                  3rd Qu.:48.50   3rd Qu.:18.70  
#>                                  Max.   :59.60   Max.   :21.50  
#>                                  NA's   :2       NA's   :2      
#>  flipper_length_mm  body_mass_g       sex           year     
#>  Min.   :172.0     Min.   :2700   female:165   Min.   :2007  
#>  1st Qu.:190.0     1st Qu.:3550   male  :168   1st Qu.:2007  
#>  Median :197.0     Median :4050   NA's  : 11   Median :2008  
#>  Mean   :200.9     Mean   :4202                Mean   :2008  
#>  3rd Qu.:213.0     3rd Qu.:4750                3rd Qu.:2009  
#>  Max.   :231.0     Max.   :6300                Max.   :2009  
#>  NA's   :2         NA's   :2

给出了一些有用的信息，但是主要给了很多对鸟瞰数据并不十分有效的分位数描述性统计量。

推荐使用：tidyverse 下的 glimpse

glimpse(penguins)
#> Rows: 344
#> Columns: 8
#> $ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, A…
#> $ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torge…
#> $ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.…
#> $ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.…
#> $ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, …
#> $ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 347…
#> $ sex               <fct> male, female, female, NA, female, male, female, m…
#> $ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2…

?penguins： 「R，向我解释/告诉我关于？后面数据集/函数/…的详细信息。」

Among the variables in penguins are:

1. species: a penguin’s species (Adelie, Chinstrap, or Gentoo).

2. flipper_length_mm: length of a penguin’s flipper, in millimeters.

3. body_mass_g: body mass of a penguin, in grams.

To learn more about penguins, open its help page by running ?penguins.

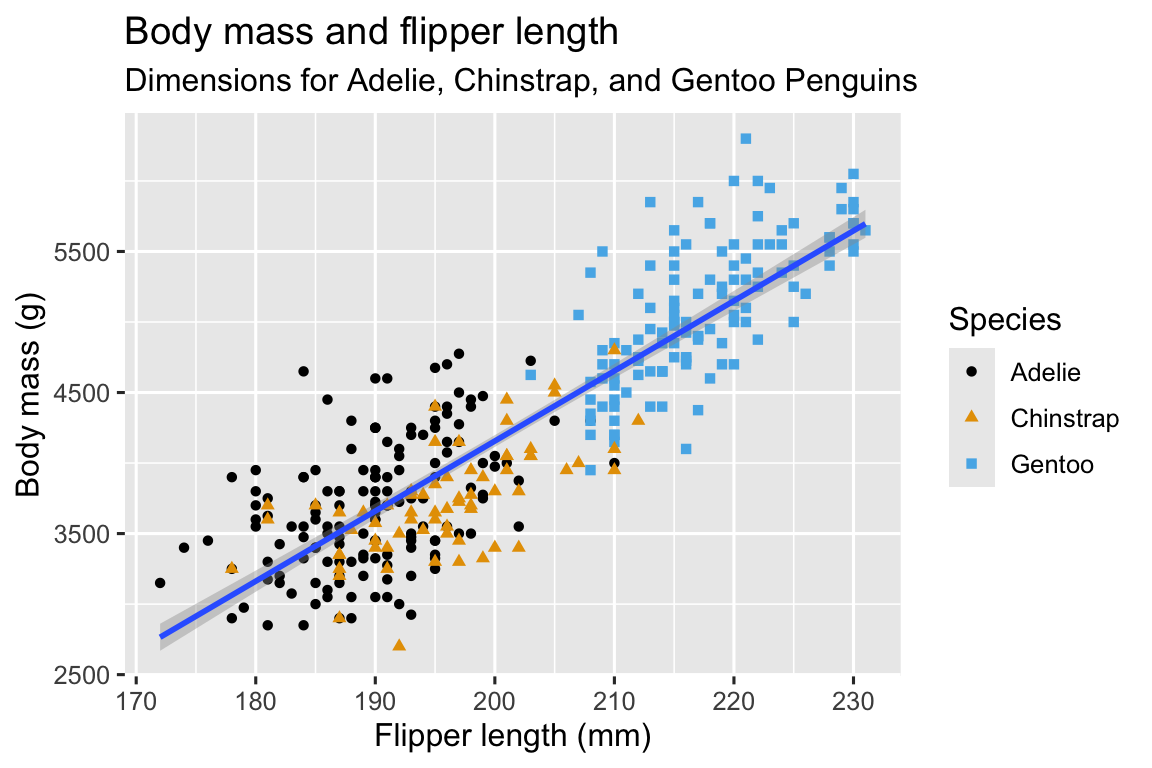
2.3.3 目标图

Our ultimate goal in this chapter is to recreate the following visualization displaying the relationship between flipper lengths and body masses of these penguins, taking into consideration the species of the penguin.

2.3.4 Creating a ggplot 绘画开始

Let’s recreate this plot step-by-step.

With ggplot2, you begin a plot with the function ggplot(), defining a plot object that you then add layers to. The first argument of ggplot() is the dataset to use in the graph and so ggplot(data = penguins) creates an empty graph that is primed to display the penguins data, but since we haven’t told it how to visualize it yet, for now it’s empty. This is not a very exciting plot, but you can think of it like an empty canvas you’ll paint the remaining layers of your plot onto.

ggplot(data = penguins)

Next, we need to tell ggplot() how the information from our data will be visually represented.

The mapping argument of the ggplot() function defines how variables in your dataset are mapped to visual properties (aesthetics) of your plot.

The mapping argument is always defined in the aes() function, and the x and y arguments of aes() specify which variables to map to the x and y axes.

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g)
)

Our empty canvas now has more structure – it’s clear where flipper lengths will be displayed (on the x-axis) and where body masses will be displayed (on the y-axis). But the penguins themselves are not yet on the plot. This is because we have not yet articulated, in our code, how to represent the observations from our data frame on our plot.

To do so, we need to define a geom: the geometrical object that a plot uses to represent data. These geometric objects are made available in ggplot2 with functions that start with geom_. People often describe plots by the type of geom that the plot uses. For example, bar charts use bar geoms (geom_bar()), line charts use line geoms (geom_line()), boxplots use boxplot geoms (geom_boxplot()), scatterplots use point geoms (geom_point()), and so on.

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g)
) +
  geom_point()
#> Warning: Removed 2 rows containing missing values or values outside the scale range
#> (`geom_point()`).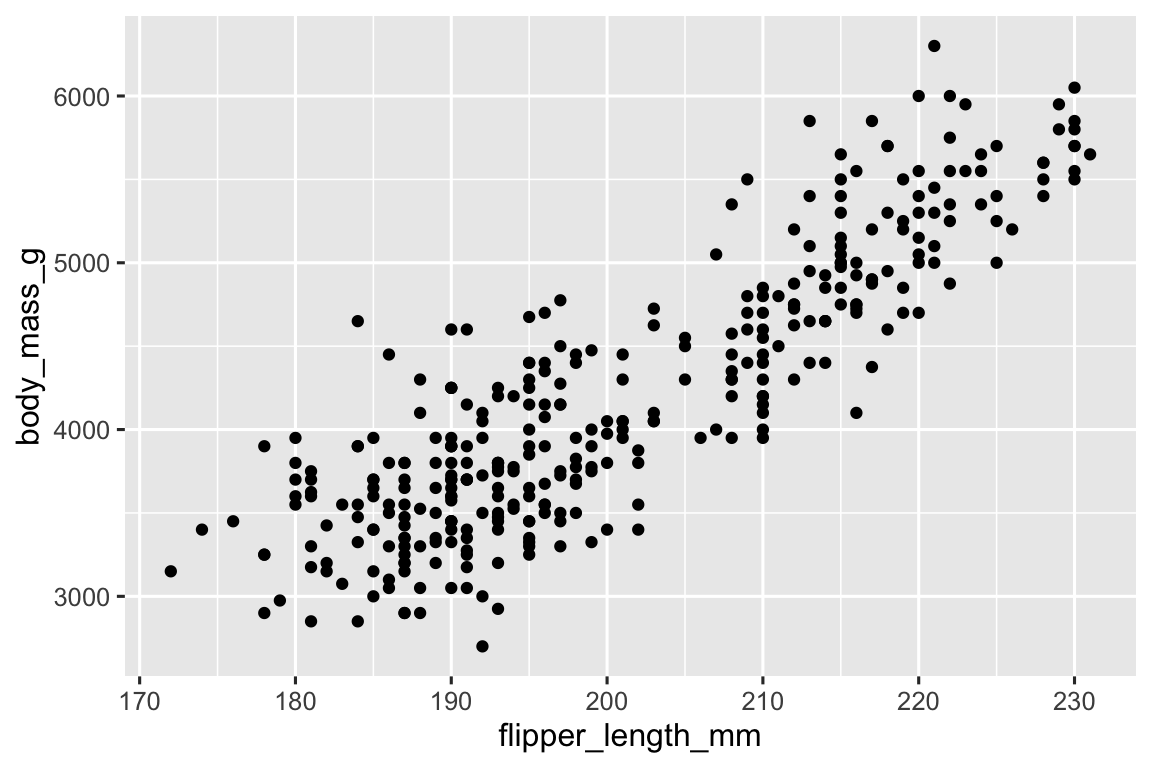

2.3.4.1 清晰的语法逻辑：函数参数与绘画步骤的区分

注意！在看生成的图之前，请仔细观察代码。回答下面3个问题:

1. ggplot 函数, 右括号 “)” 结束在哪里？括号之内包含的是什么？参数还是函数？
2. ggplot 函数结束后，出现了什么符号？发生了什么？
3. geom_()是什么？起到了什么功能？

回答这3个问题的目的是回答这个问题：

分清参数，函数，依照什么准则，什么标准，决定将其放在代码的哪个部分？

2.3.5 搜索资源 + 独立思考 + 批判接收

我认为B站最清楚的讲解视频之一： Lizongzhang老师的视频

ggplot2 语法结构 作者: Lizongzhang - Bilibili

基于你对ggplot2所了解的，看她前几分钟的讲解，思考：

1. 哪些部分说得清楚，对我们加深理解有益？
2. 哪些部分和我们此刻正在介绍的不同？

2.3.5.1 支线剧情： regression

既然我们的问题是 flipper length 和 body mass 的关系，同时，我们通过上图看到了明显的正线性相关性，那么，我们可以潜在的建立线性回归模型。

Regression analysis ends here. A complete approach will be presented elsewhere. 为了不绕开画图这条主线，在这里暂时只作思路演示。

2.3.5.2 支线剧情： dataset exploration: descriptive

Before conducting any further regression or even further visualization, it is just sensible to quickly get a sense of the response variables and explanatory variables of interest. The modern way to do that is moderndive and skimr.

library(moderndive)
library(skimr)

penguins |>
  select(flipper_length_mm, body_mass_g) |>
  skim()

Data summary

Name	select(penguins, flipper_…
Number of rows	344
Number of columns	2
_______________________
Column type frequency:
numeric	2
________________________
Group variables	None

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
flipper_length_mm	2	0.99	200.92	14.06	172	190	197	213	231	▂▇▃▅▂
body_mass_g	2	0.99	4201.75	801.95	2700	3550	4050	4750	6300	▃▇▆▃▂

autoReg

library(autoReg)

gaze(data = penguins)
#> ——————————————————————————————————————————————
#>        name          levels        stats      
#> ——————————————————————————————————————————————
#> species            Adelie          152 (44.2%) 
#>                    Chinstrap        68 (19.8%) 
#>                    Gentoo          124 (36.0%) 
#> island             Biscoe          168 (48.8%) 
#>                    Dream           124 (36.0%) 
#>                    Torgersen        52 (15.1%) 
#> bill_length_mm     Mean ± SD        43.9 ± 5.5 
#> bill_depth_mm      Mean ± SD        17.2 ± 2.0 
#> flipper_length_mm  Mean ± SD      200.9 ± 14.1 
#> body_mass_g        Mean ± SD    4201.8 ± 802.0 
#> sex                female          165 (49.5%) 
#>                    male            168 (50.5%) 
#> year               Mean ± SD      2008.0 ± 0.8 
#> ——————————————————————————————————————————————

(penguins_describe <- gaze(data = penguins) |> myft())

name	levels	stats
species	Adelie	152 (44.2%)
	Chinstrap	68 (19.8%)
	Gentoo	124 (36.0%)
island	Biscoe	168 (48.8%)
	Dream	124 (36.0%)
	Torgersen	52 (15.1%)
bill_length_mm	Mean ± SD	43.9 ± 5.5
bill_depth_mm	Mean ± SD	17.2 ± 2.0
flipper_length_mm	Mean ± SD	200.9 ± 14.1
body_mass_g	Mean ± SD	4201.8 ± 802.0
sex	female	165 (49.5%)
	male	168 (50.5%)
year	Mean ± SD	2008.0 ± 0.8

2.3.5.3 回到图像

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g)
) +
  geom_point()
#> Warning: Removed 2 rows containing missing values or values outside the scale range
#> (`geom_point()`).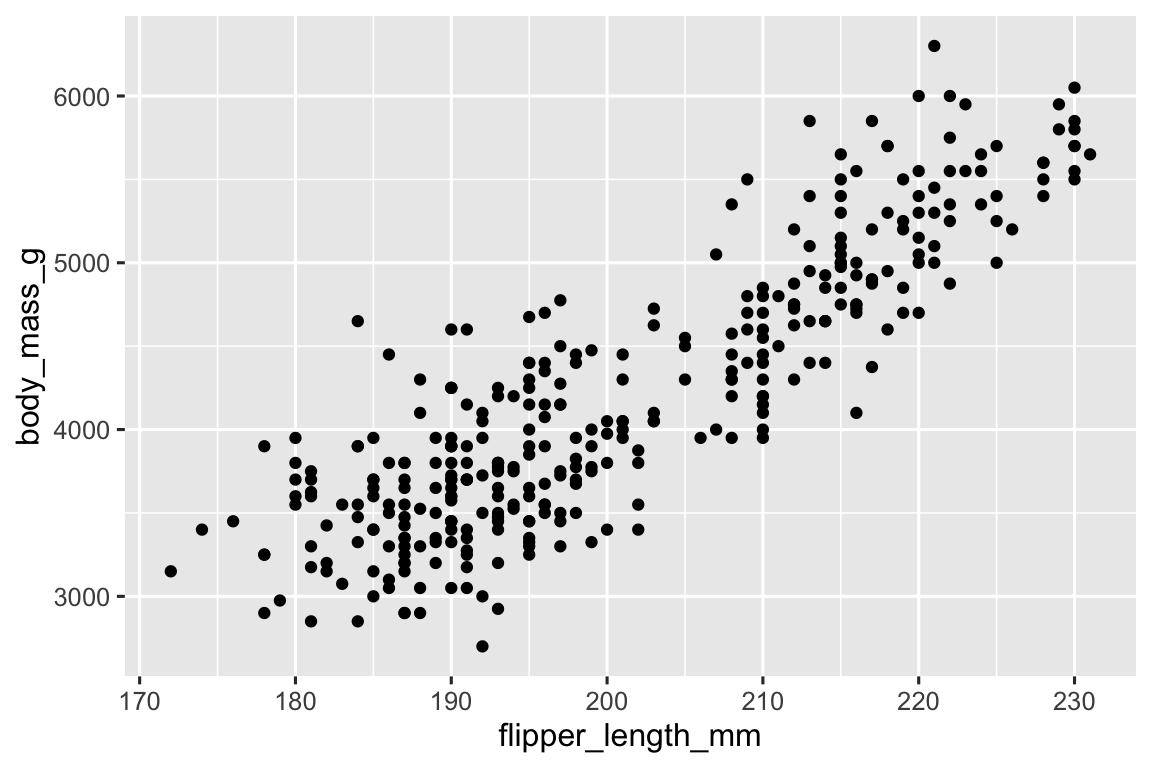

Now we have something that looks like what we might think of as a “scatterplot”. It doesn’t yet match our “ultimate goal” plot, but using this plot we can start answering the question that motivated our exploration: “What does the relationship between flipper length and body mass look like?” The relationship appears to be positive (as flipper length increases, so does body mass), fairly linear (the points are clustered around a line instead of a curve), and moderately strong (there isn’t too much scatter around such a line). Penguins with longer flippers are generally larger in terms of their body mass.

Before we add more layers to this plot, let’s pause for a moment and review the warning message we got:

Removed 2 rows containing missing values (geom_point()).

We’re seeing this message because there are two penguins in our dataset with missing body mass and/or flipper length values and ggplot2 has no way of representing them on the plot without both of these values. Like R, ggplot2 subscribes to the philosophy that missing values should never silently go missing. This type of warning is probably one of the most common types of warnings you will see when working with real data – missing values are a very common issue and you’ll learn more about them throughout the book, particularly in ?sec-missing-values. For the remaining plots in this chapter we will suppress this warning so it’s not printed alongside every single plot we make.

2.3.6 Adding aesthetics and layers

Scatterplots are useful for displaying the relationship between two numerical variables, but it’s always a good idea to be skeptical of any apparent relationship between two variables and ask if there may be other variables that explain or change the nature of this apparent relationship.

散点图 (Scatterplots) 可以很有效地展示「2个数值变量」的关系 (relationship)。

然而，看似明显的两个变量之间关系是可疑的。看 看是否有其它变量可以解释或改变这样看似明显的关系，往往是个好主意。

For example, does the relationship between flipper length and body mass differ by species? Let’s incorporate species into our plot and see if this reveals any additional insights into the apparent relationship between these variables. We will do this by representing species with different colored points.

想要解决的问题：

不同企鹅种类，蹼长和体重的关系是不是也不同？

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g, color = species)
) +
  geom_point()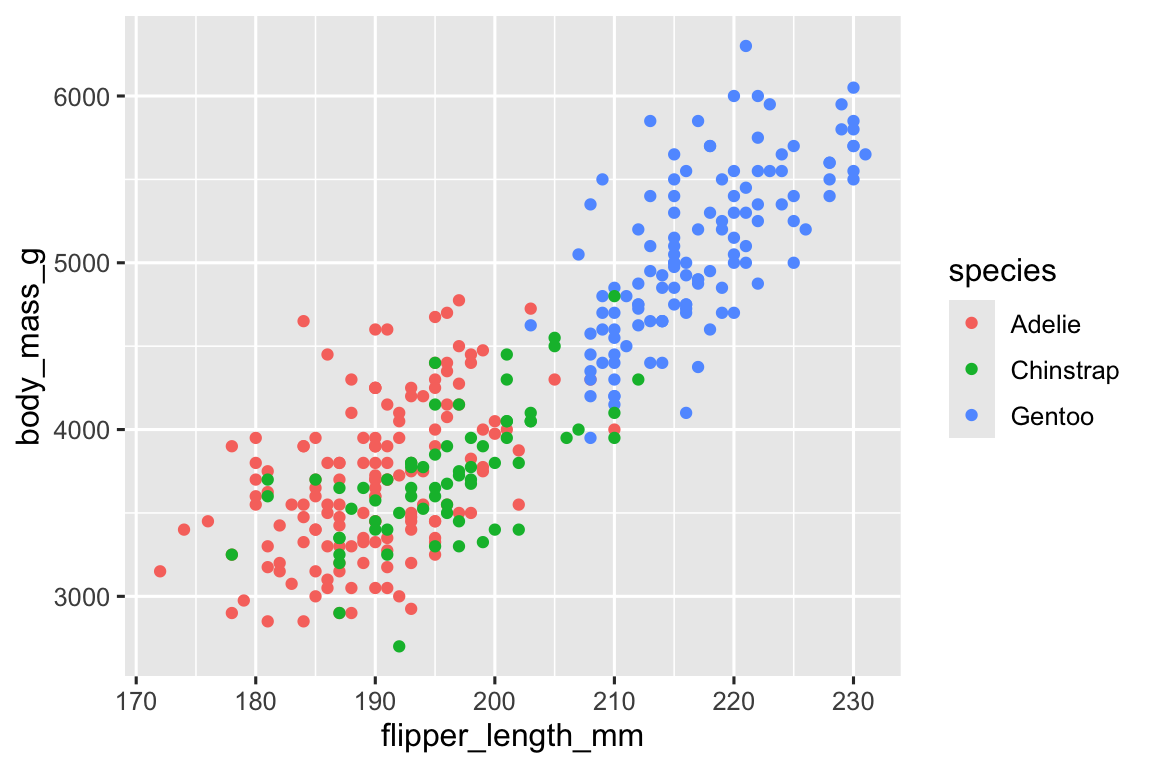 

2.4 散点图拟合：global vs. local aes()

加一层: geom_smooth(). 基于线性模型拟合： method = "lm".

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g, color = species)
) +
  geom_point() +
  geom_smooth(method = "lm")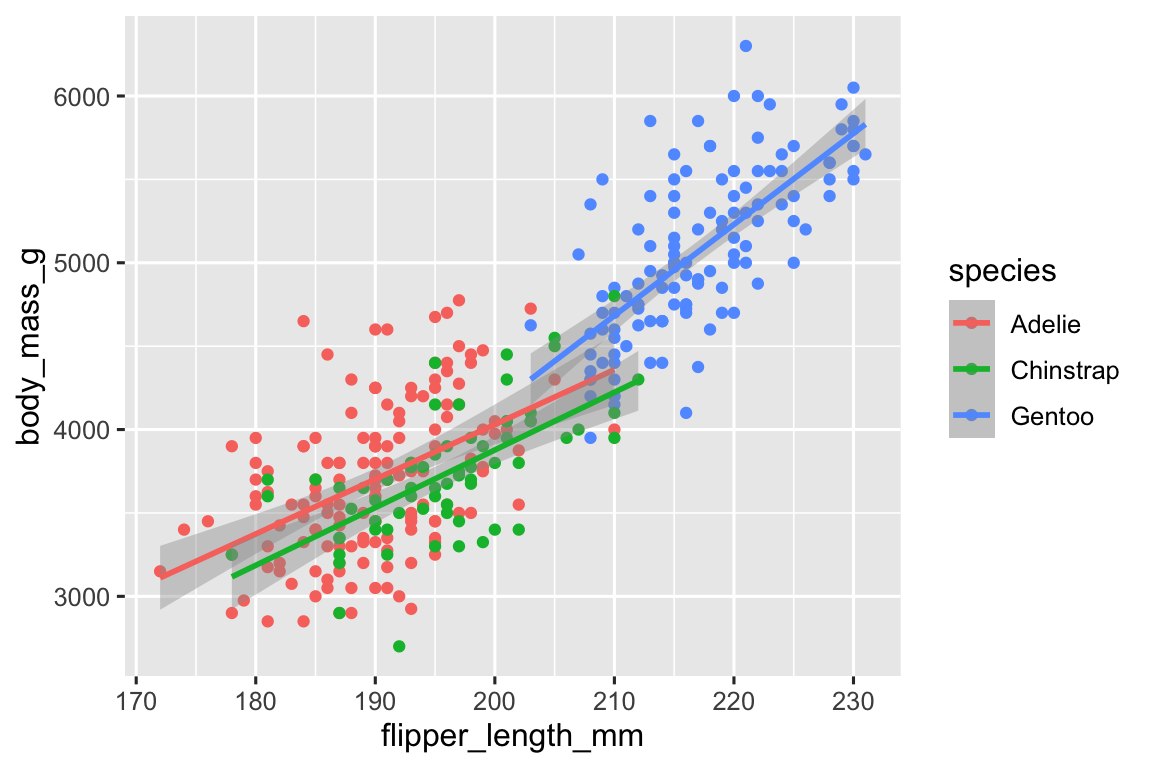

新的代码只是在原代码基础上 + geom_smooth(method = "lm")而已。画 油画逻辑，在原画上画一层拟合。但 是，看到这个图，你是否会有一个疑问：

为什么上图的拟合线段是分别对不同企鹅进行的，出现3条，而不是1条线对所有点拟合?

只是在原代码基础上 + geom_smooth(method = "lm")而已。并 没有告诉 geom_smooth() 我要对每一个企鹅种类分别拟合啊？

首先，对所有点拟合的情景能不能实现？是怎么实现的呢？如下图可见：

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g)
) +
  geom_point(mapping = aes(color = species)) +
  geom_smooth(method = "lm")
#> `geom_smooth()` using formula = 'y ~ x'
#> Warning: Removed 2 rows containing non-finite outside the scale range
#> (`stat_smooth()`).
#> Warning: Removed 2 rows containing missing values or values outside the scale range
#> (`geom_point()`).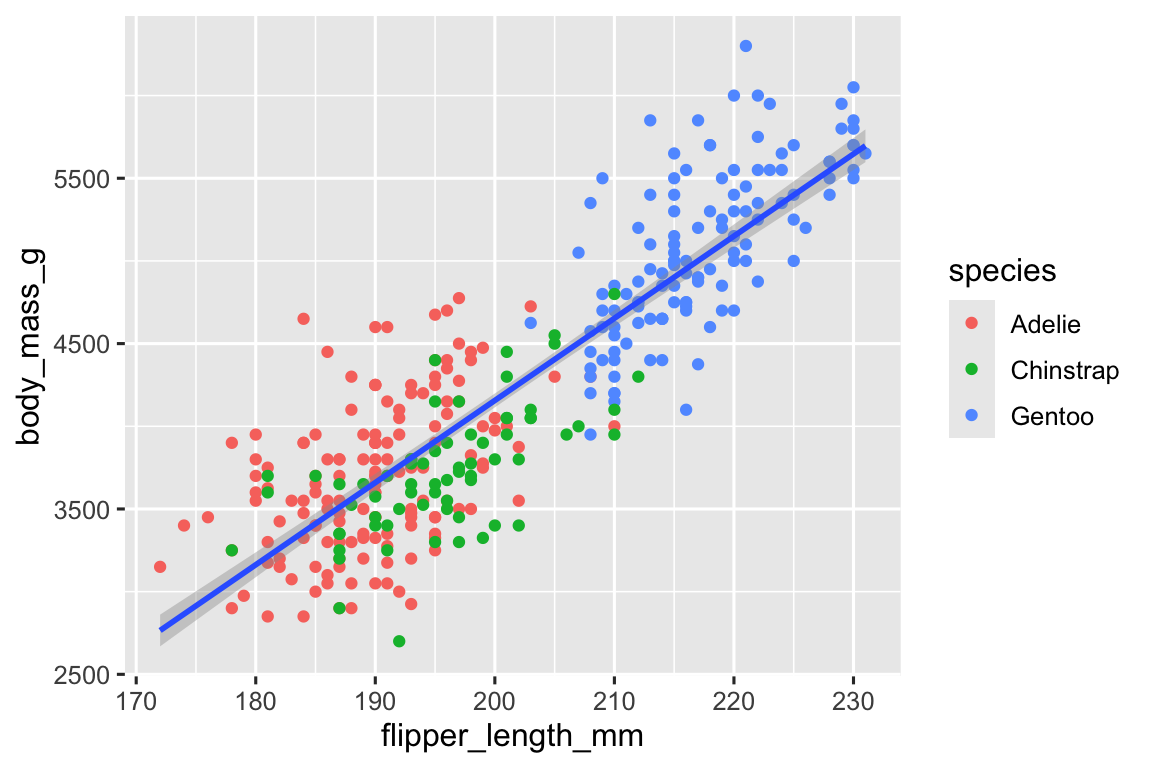

差别在哪里？到 底发生了什么？

回答这个问题所带出的信息，非常重要。

为方便比较，我们把2图代码摆在一起：

分段拟合代码：

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g, 
                color = species)
) +
  geom_point() +
  geom_smooth(method = "lm")

整体拟合代码：

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g)
) +
  geom_point(mapping = aes(color = species)) +
  geom_smooth(method = "lm")

找不同！唯一的不同：color = species 位置。其 它代码完全相同。

因此我们可以推测，2图呈现的不同，是由aes()的位置在ggplot()中还是在geom_()中决定的。

直接给出直观的答案:

下面代码，aes(color = species) 定义在「第一步骤主函数」 ggplot() 中。

= 这使得，按企鹅种类上色的指令具备全局权限。事实上，

2.5 无比关键的语法逻辑！不知为何其它教程很少涉及？

• mapping = aes() 的位置 - 审美参数映射逻辑的全局(global)和本地(local)权限

Hadley Wickham：

When aesthetic mappings are defined in ggplot(), at the global level, they’re passed down to each of the subsequent geom layers of the plot. However, each geom function in ggplot2 can also take a mapping argument, which allows for aesthetic mappings at the local level that are added to those inherited from the global level. Since we want points to be colored based on species but don’t want the lines to be separated out for them, we should specify color = species for geom_point() only.

R与统计的翻译：

当“审美映射”的要求在 ggplot()函数内定义，这些审美要求（比如， color = species）就具有了「全局」(global) 权限。这些要求会被传递到每个接下来的 geom_ 中。

然而，每个geom函数也可以声明mapping, 允许审美映射出现在「本地」(local). 此时，全局当中没有定义的审美映射要求，在本地定义了，geom_()执行起来自然就只看自身定义的要求即可。

2.5.1 【R与统计的解读】清晰拆解语法逻辑

到底发生了什么？分段拟合图

• 在ggplot()里要求的审美映射，比如color = species, 如果后续geom_()中没有再定义 : 比如，仅仅是 geom_smooth(method = "lm")，

  那么相当于实际上执行了的是 geom_smooth(color = species, method = "lm")。也就是 geom_() 会继承 ggplot() 里全局定义的审美。

自己无审美定义，继承color = species，因此产出按种类分段拟合：

A. 分段拟合

#  color = species 定义在 ggplot()的 mapping 里
ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g, 
                color = species) # 要求 color = species，位置：全局
) +
  geom_point() + #没定义映射，继承 color = species，按种类上色
  geom_smooth(method = "lm") #自己无审美定义，继承 color = species，产出按种类分段拟合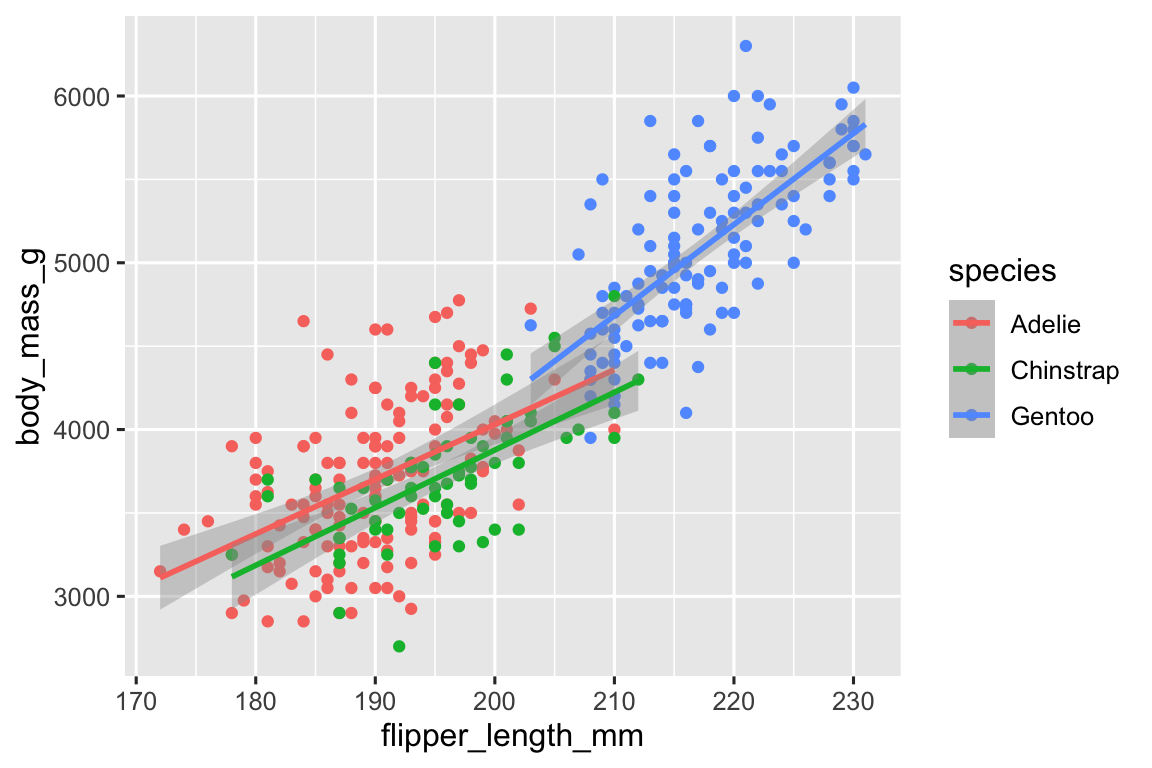

怎么做到的？整体拟合图

审美映射可以直接在geom_()中定义 : 比如, geom_point(mapping = aes(color = species))

运行完这一步后， +geom_smooth(method = "lm")，geom_() 会去 ggplot() 找全局定义的审美，发现只有坐标轴变量要求 x = flipper_length_mm, y = body_mass_g，没有按种类上色的要求。因 此，拟合命令当然也无额外要求。

定义在 geom_point()里的审美与自己无关 （“我们都是平级，我只听总部 ggplot() 的。你爱什么审美什么审美。你和我同级，你的要求我无需遵守”）。

B. 整体拟合

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g) #没定义 color = species
) +
  geom_point(mapping = aes(color = species)) + #此时才定义的审美要求：color = species
  geom_smooth(method = "lm") #拟合线时没有定义审美要求，
#看ggplot()全局,也没有color =species的要求。
#好，没有按种类分别操作的要求，那就对全体数据点拟合。
#geom_point() 里定义了？你和我同级，你的要求我无需遵守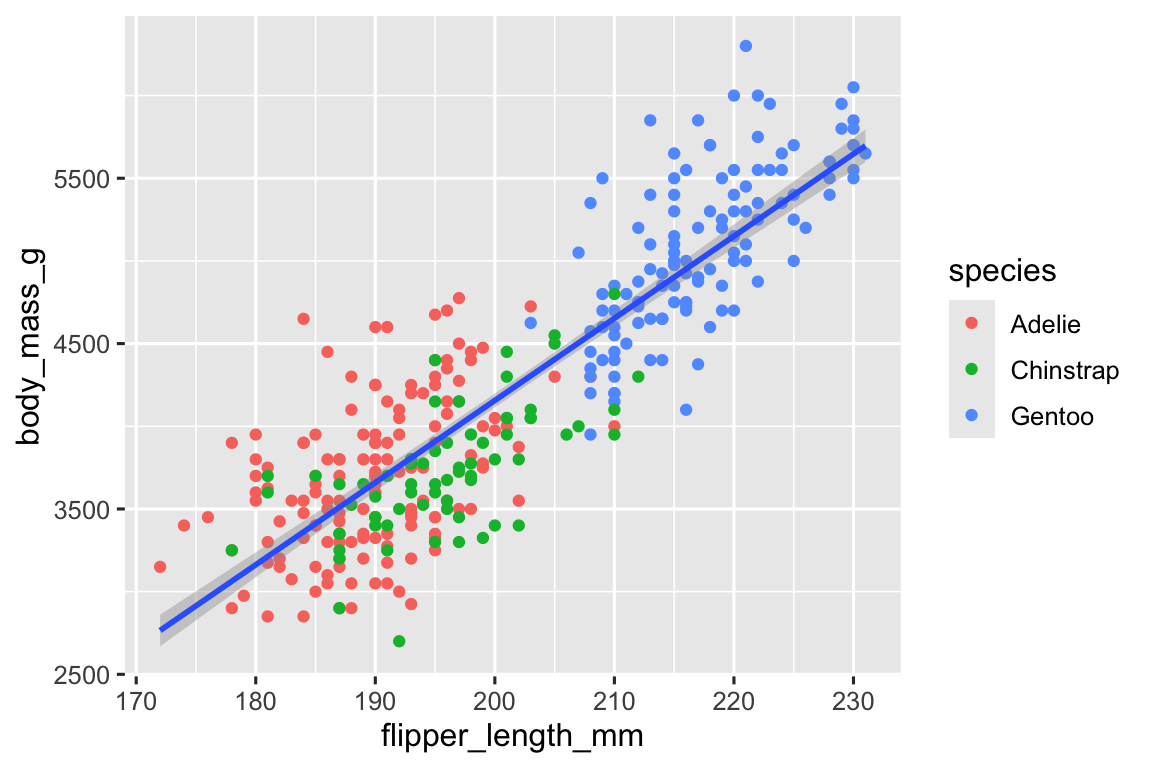

It’s generally not a good idea to represent information using only colors on a plot, as people perceive colors differently due to color blindness or other color vision differences. Therefore, in addition to color, we can also map species to the shape aesthetic.

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g)
) +
  geom_point(mapping = aes(color = species, shape = species)) +
  geom_smooth(method = "lm")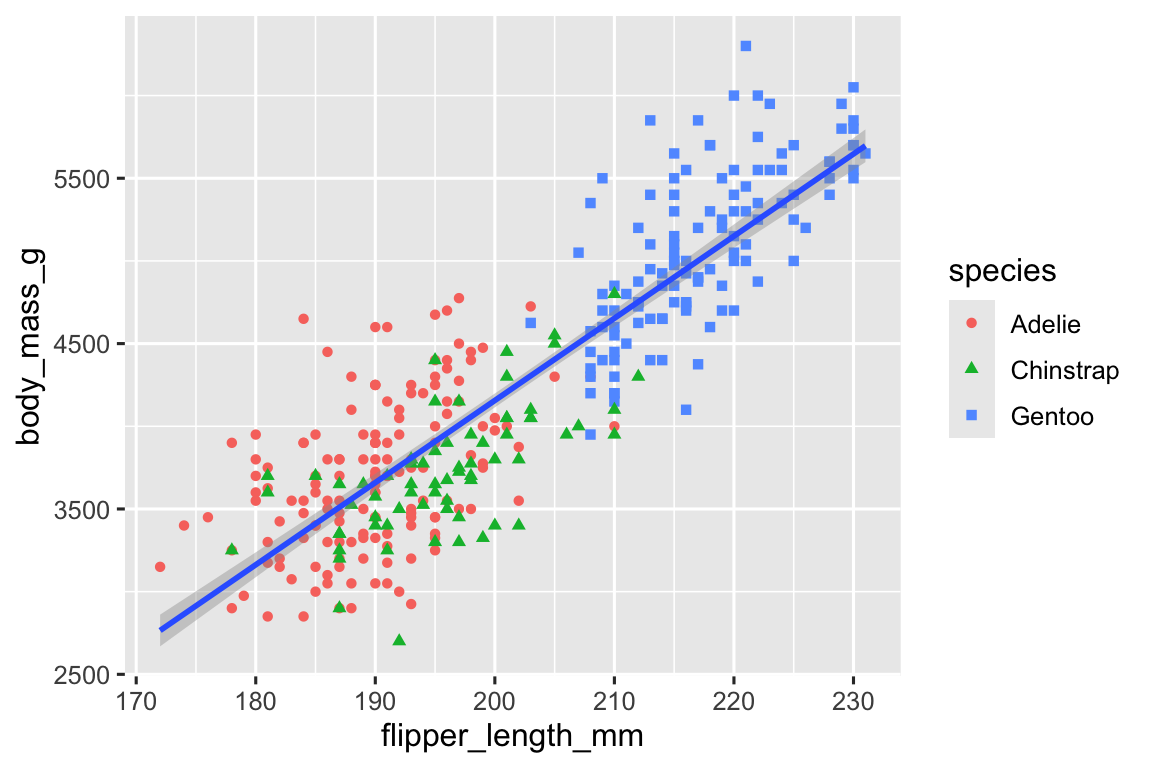

Note that the legend is automatically updated to reflect the different shapes of the points as well.

And finally, we can improve the labels of our plot using the labs() function in a new layer. Some of the arguments to labs() might be self explanatory: title adds a title and subtitle adds a subtitle to the plot. Other arguments match the aesthetic mappings, x is the x-axis label, y is the y-axis label, and color and shape define the label for the legend. In addition, we can improve the color palette to be colorblind safe with the scale_color_colorblind() function from the ggthemes package.

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g)
) +
  geom_point(aes(color = species, shape = species)) +
  geom_smooth(method = "lm") +
  labs(
    title = "Body mass and flipper length",
    subtitle = "Dimensions for Adelie, Chinstrap, and Gentoo Penguins",
    x = "Flipper length (mm)", y = "Body mass (g)",
    color = "Species", shape = "Species"
  ) +
  scale_color_colorblind()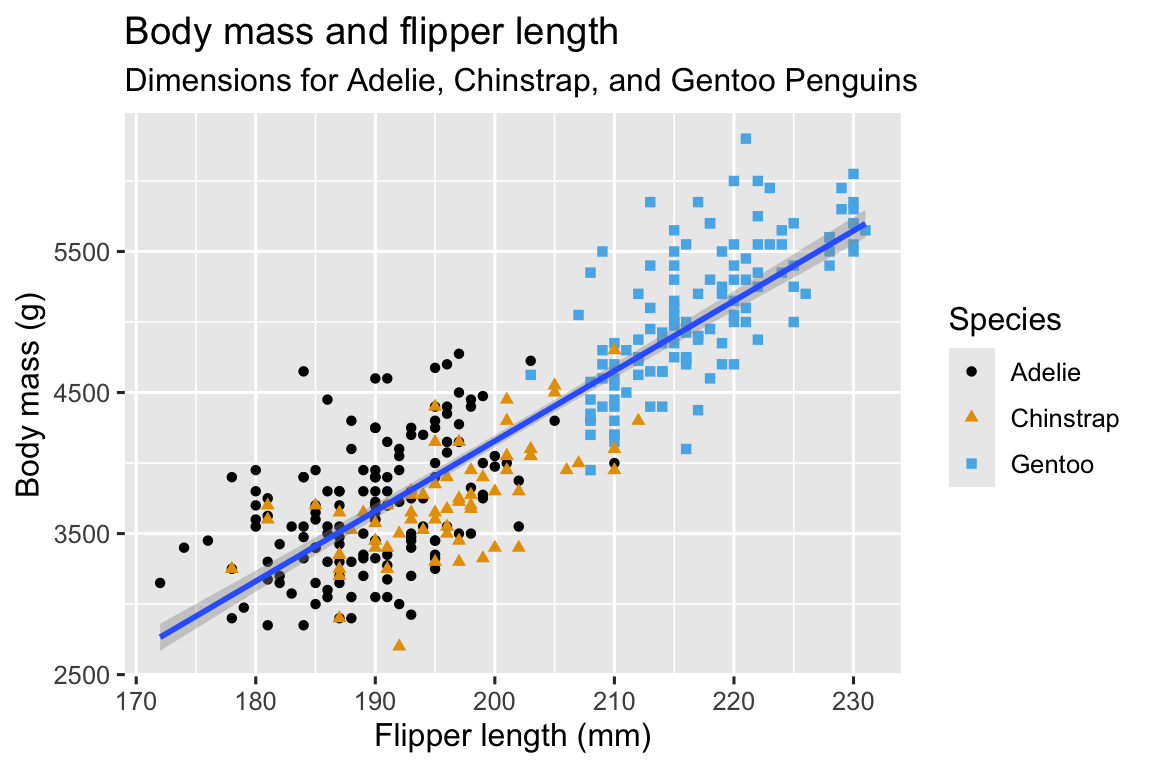

We finally have a plot that perfectly matches our “ultimate goal”!

额外：

按岛呢？先 看一下岛的基本信息：

table(penguins$island)
#> 
#>    Biscoe     Dream Torgersen 
#>       168       124        52

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g, color = island)
) +
  geom_point()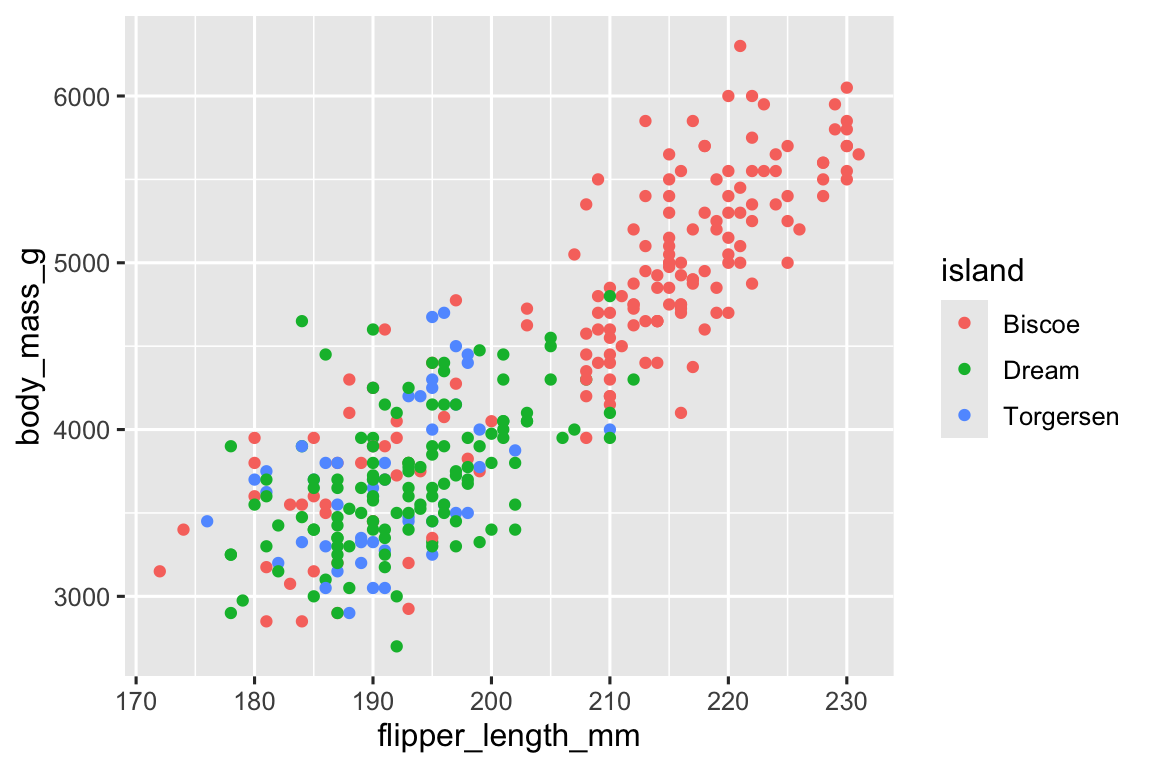

对比： 「所有的Gentoo企鹅都在Biscoe岛上，Biscoe岛上不只有Gentoo企鹅」

验证：

penguins |> 
  filter(species == "Gentoo")
#> # A tibble: 124 × 8
#>   species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
#>   <fct>   <fct>           <dbl>         <dbl>             <int>       <int>
#> 1 Gentoo  Biscoe           46.1          13.2               211        4500
#> 2 Gentoo  Biscoe           50            16.3               230        5700
#> 3 Gentoo  Biscoe           48.7          14.1               210        4450
#> 4 Gentoo  Biscoe           50            15.2               218        5700
#> 5 Gentoo  Biscoe           47.6          14.5               215        5400
#> 6 Gentoo  Biscoe           46.5          13.5               210        4550
#> # ℹ 118 more rows
#> # ℹ 2 more variables: sex <fct>, year <int>
# 124 obs

penguins |> 
  filter(species == "Gentoo" & island == "Biscoe")
#> # A tibble: 124 × 8
#>   species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
#>   <fct>   <fct>           <dbl>         <dbl>             <int>       <int>
#> 1 Gentoo  Biscoe           46.1          13.2               211        4500
#> 2 Gentoo  Biscoe           50            16.3               230        5700
#> 3 Gentoo  Biscoe           48.7          14.1               210        4450
#> 4 Gentoo  Biscoe           50            15.2               218        5700
#> 5 Gentoo  Biscoe           47.6          14.5               215        5400
#> 6 Gentoo  Biscoe           46.5          13.5               210        4550
#> # ℹ 118 more rows
#> # ℹ 2 more variables: sex <fct>, year <int>
# 124 obs

penguins |> 
  filter(island == "Biscoe")
#> # A tibble: 168 × 8
#>   species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
#>   <fct>   <fct>           <dbl>         <dbl>             <int>       <int>
#> 1 Adelie  Biscoe           37.8          18.3               174        3400
#> 2 Adelie  Biscoe           37.7          18.7               180        3600
#> 3 Adelie  Biscoe           35.9          19.2               189        3800
#> 4 Adelie  Biscoe           38.2          18.1               185        3950
#> 5 Adelie  Biscoe           38.8          17.2               180        3800
#> 6 Adelie  Biscoe           35.3          18.9               187        3800
#> # ℹ 162 more rows
#> # ℹ 2 more variables: sex <fct>, year <int>
# 168 obs

Interpretation:

1. according to the row numbers of the subset 1 & 2, we can see that all Gentoo penguins observed live in Biscoe island .
2. according to the row numbers of the subset 2 & 3, we can see that 168 penguins live in Biscoe island, renders 42 of them are penguins that are not Gentoo.

These observations explains what Plot by-species and Plot by-lsland suggests.

2.5.2 Exercises

1. How many rows are in penguins? How many columns?

2. What does the bill_depth_mm variable in the penguins data frame describe? Read the help for ?penguins to find out.

3. Make a scatterplot of bill_depth_mm vs. bill_length_mm. That is, make a scatterplot with bill_depth_mm on the y-axis and bill_length_mm on the x-axis. Describe the relationship between these two variables.

4. What happens if you make a scatterplot of species vs. bill_depth_mm? What might be a better choice of geom?

5. Why does the following give an error and how would you fix it?

   ggplot(data = penguins) + 
     geom_point()

6. What does the na.rm argument do in geom_point()? What is the default value of the argument? Create a scatterplot where you successfully use this argument set to TRUE.

7. Add the following caption to the plot you made in the previous exercise: “Data come from the palmerpenguins package.” Hint: Take a look at the documentation for labs().

8. Recreate the following visualization. What aesthetic should bill_depth_mm be mapped to? And should it be mapped at the global level or at the geom level?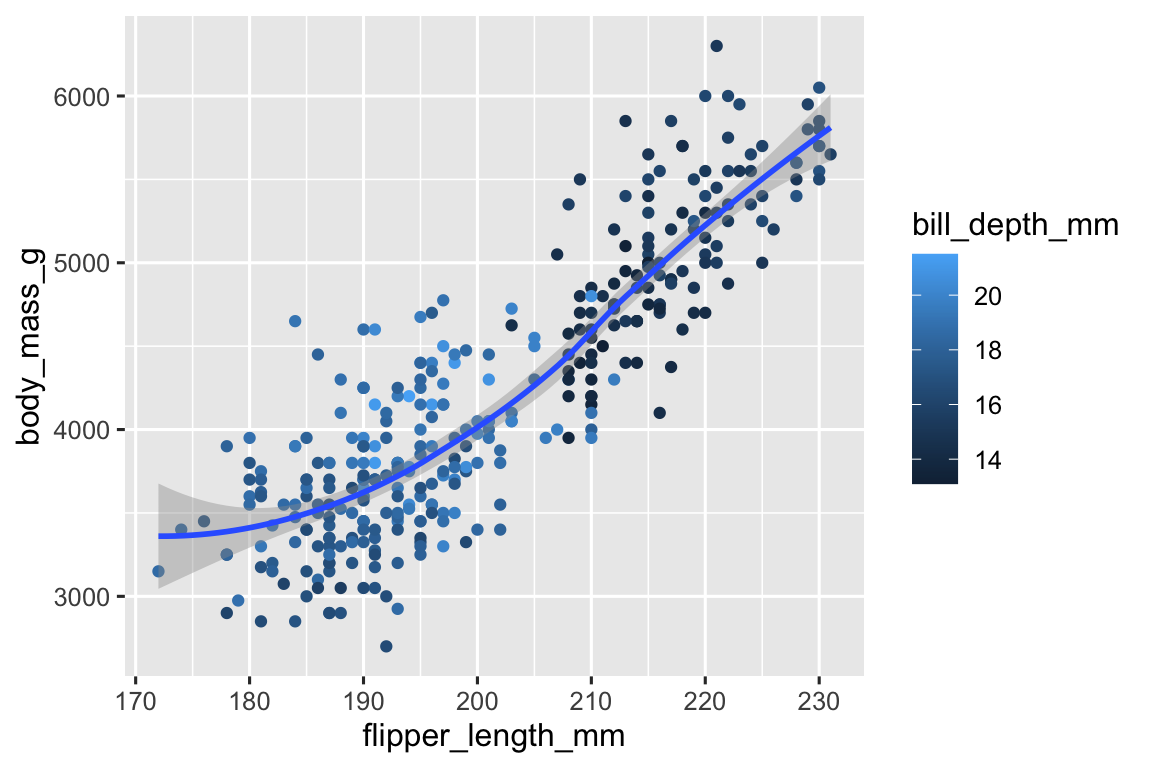

   

9. Run this code in your head and predict what the output will look like. Then, run the code in R and check your predictions.

   ggplot(
     data = penguins,
     mapping = aes(x = flipper_length_mm, y = body_mass_g, color = island)
   ) +
     geom_point() +
     geom_smooth(se = FALSE)

10. Will these two graphs look different? Why/why not?

    ggplot(
      data = penguins,
      mapping = aes(x = flipper_length_mm, y = body_mass_g)
    ) +
      geom_point() +
      geom_smooth()
    
    ggplot() +
      geom_point(
        data = penguins,
        mapping = aes(x = flipper_length_mm, y = body_mass_g)
      ) +
      geom_smooth(
        data = penguins,
        mapping = aes(x = flipper_length_mm, y = body_mass_g)
      )

2.6 ggplot2 calls

As we move on from these introductory sections, we’ll transition to a more concise expression of ggplot2 code. So far we’ve been very explicit, which is helpful when you are learning:

ggplot(
  data = penguins,
  mapping = aes(x = flipper_length_mm, y = body_mass_g)
) +
  geom_point()

Typically, the first one or two arguments to a function are so important that you should know them by heart. The first two arguments to ggplot() are data and mapping, in the remainder of the book, we won’t supply those names. That saves typing, and, by reducing the amount of extra text, makes it easier to see what’s different between plots. That’s a really important programming concern that we’ll come back to in ?sec-functions.

Rewriting the previous plot more concisely yields:

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) + 
  geom_point()

In the future, you’ll also learn about the pipe, |>, which will allow you to create that plot with:

penguins |> 
  ggplot(aes(x = flipper_length_mm, y = body_mass_g)) + 
  geom_point()

2.7 Visualizing distributions

How you visualize the distribution of a variable depends on the type of variable: categorical or numerical.

2.7.1 A categorical variable

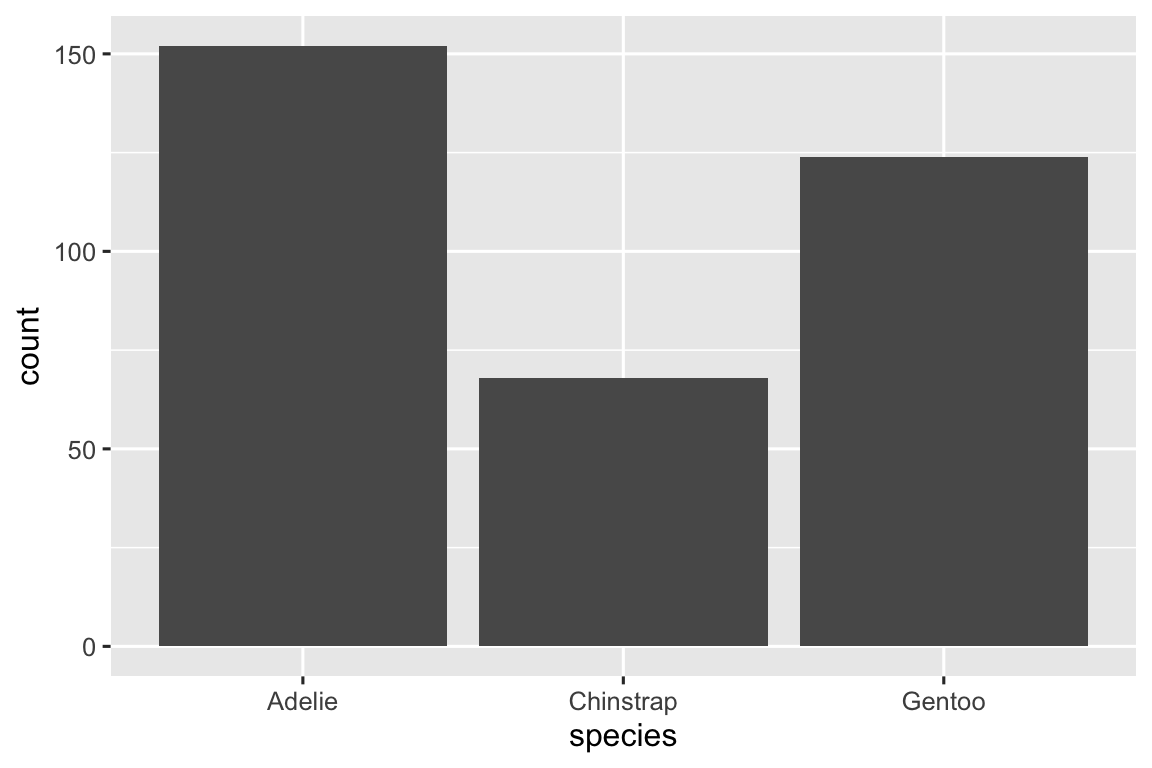
A variable is categorical if it can only take one of a small set of values. To examine the distribution of a categorical variable, you can use a bar chart. The height of the bars displays how many observations occurred with each x value.

ggplot(penguins, aes(x = species)) +
  geom_bar()

In bar plots of categorical variables with non-ordered levels, like the penguin species above, it’s often preferable to reorder the bars based on their frequencies. Doing so requires transforming the variable to a factor (how R handles categorical data) and then reordering the levels of that factor.

ggplot(penguins, aes(x = fct_infreq(species))) +
  geom_bar()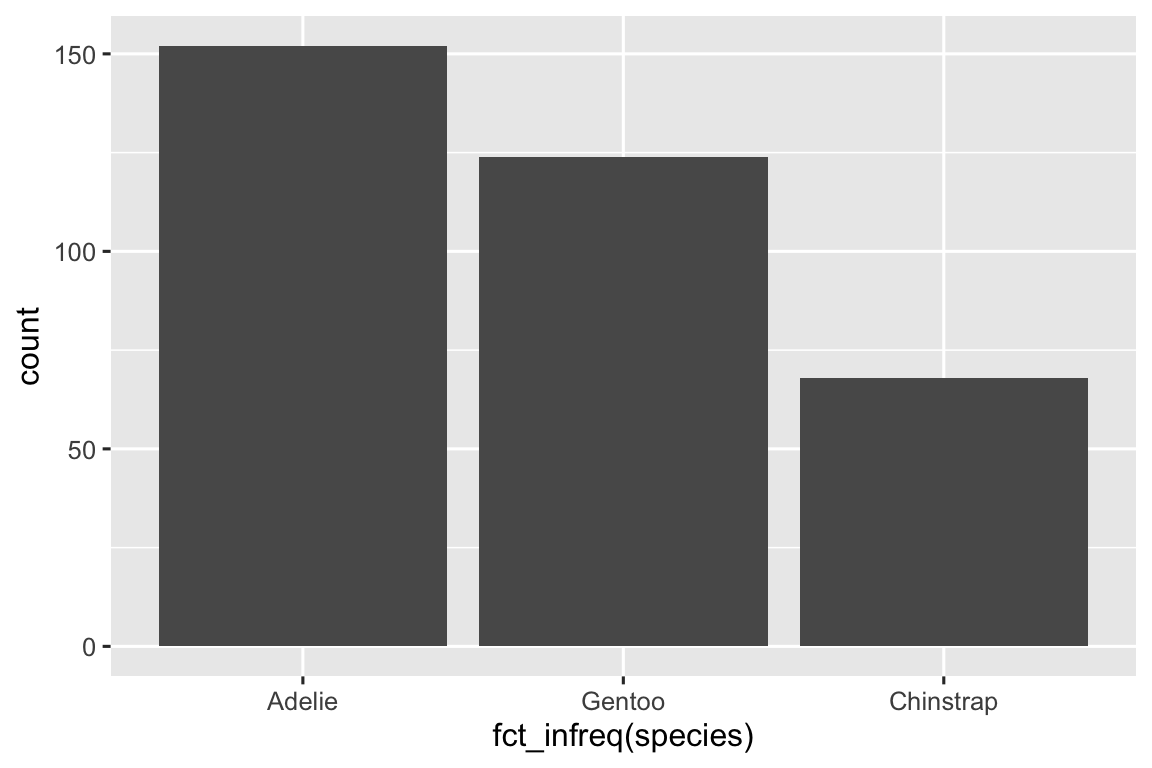

You will learn more about factors and functions for dealing with factors (like fct_infreq() shown above) in ?sec-factors.

2.7.2 A numerical variable

A variable is numerical (or quantitative) if it can take on a wide range of numerical values, and it is sensible to add, subtract, or take averages with those values. Numerical variables can be continuous or discrete.

One commonly used visualization for distributions of continuous variables is a histogram.

ggplot(penguins, aes(x = body_mass_g)) +
  geom_histogram(binwidth = 200)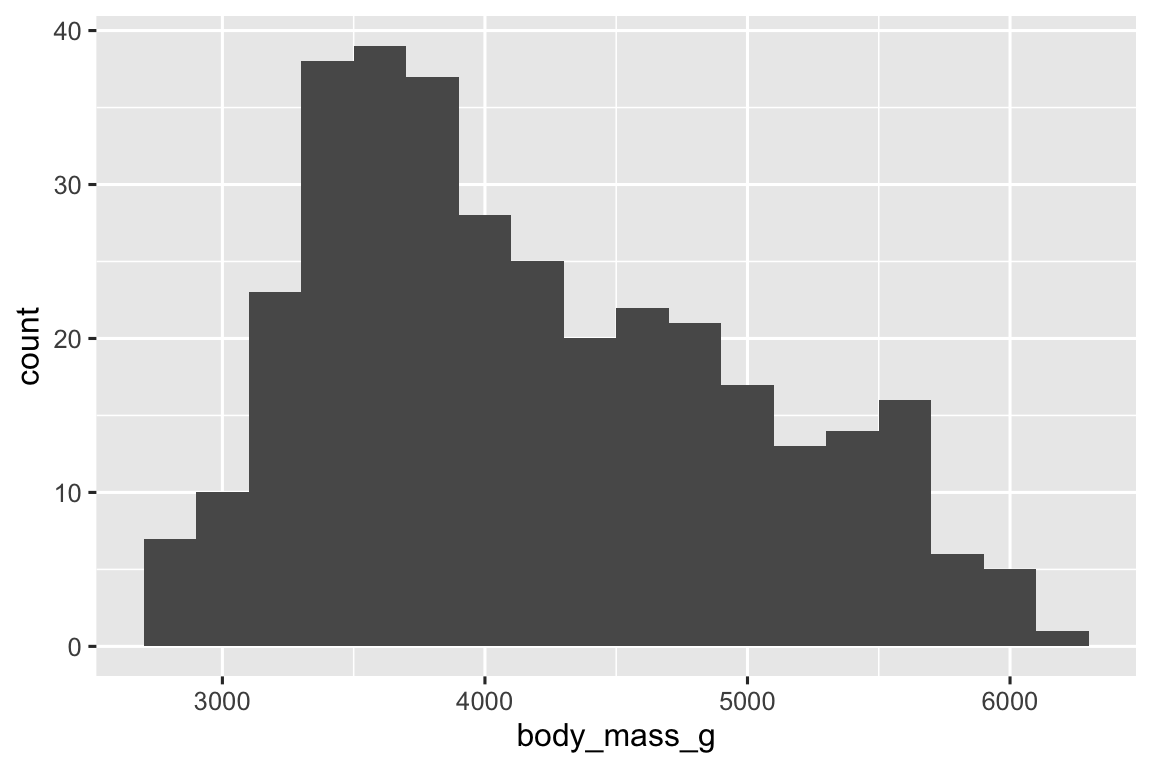

A histogram divides the x-axis into equally spaced bins and then uses the height of a bar to display the number of observations that fall in each bin. In the graph above, the tallest bar shows that 39 observations have a body_mass_g value between 3,500 and 3,700 grams, which are the left and right edges of the bar.

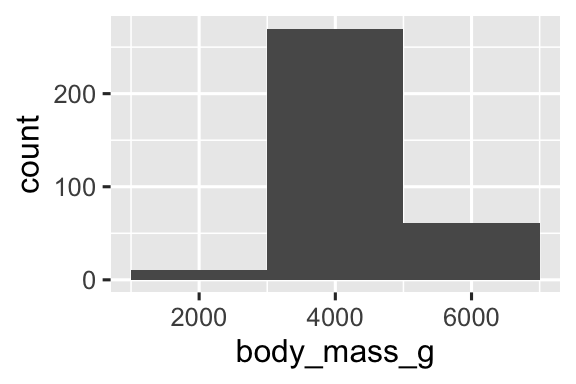
You can set the width of the intervals in a histogram with the binwidth argument, which is measured in the units of the x variable. You should always explore a variety of binwidths when working with histograms, as different binwidths can reveal different patterns. In the plots below a binwidth of 20 is too narrow, resulting in too many bars, making it difficult to determine the shape of the distribution. Similarly, a binwidth of 2,000 is too high, resulting in all data being binned into only three bars, and also making it difficult to determine the shape of the distribution. A binwidth of 200 provides a sensible balance.

ggplot(penguins, aes(x = body_mass_g)) +
  geom_histogram(binwidth = 20)
ggplot(penguins, aes(x = body_mass_g)) +
  geom_histogram(binwidth = 2000)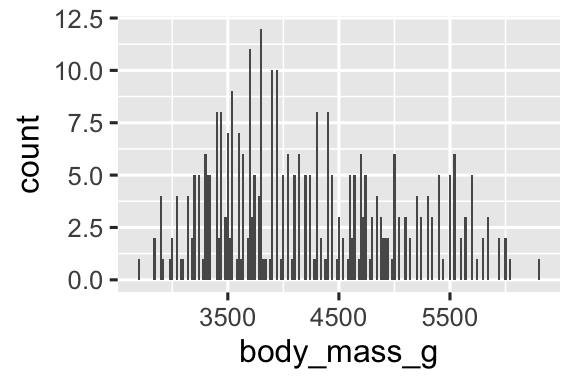

An alternative visualization for distributions of numerical variables is a density plot. A density plot is a smoothed-out version of a histogram and a practical alternative, particularly for continuous data that comes from an underlying smooth distribution. We won’t go into how geom_density() estimates the density (you can read more about that in the function documentation), but let’s explain how the density curve is drawn with an analogy. Imagine a histogram made out of wooden blocks. Then, imagine that you drop a cooked spaghetti string over it. The shape the spaghetti will take draped over blocks can be thought of as the shape of the density curve. It shows fewer details than a histogram but can make it easier to quickly glean the shape of the distribution, particularly with respect to modes and skewness.

ggplot(penguins, aes(x = body_mass_g)) +
  geom_density()
#> Warning: Removed 2 rows containing non-finite outside the scale range
#> (`stat_density()`).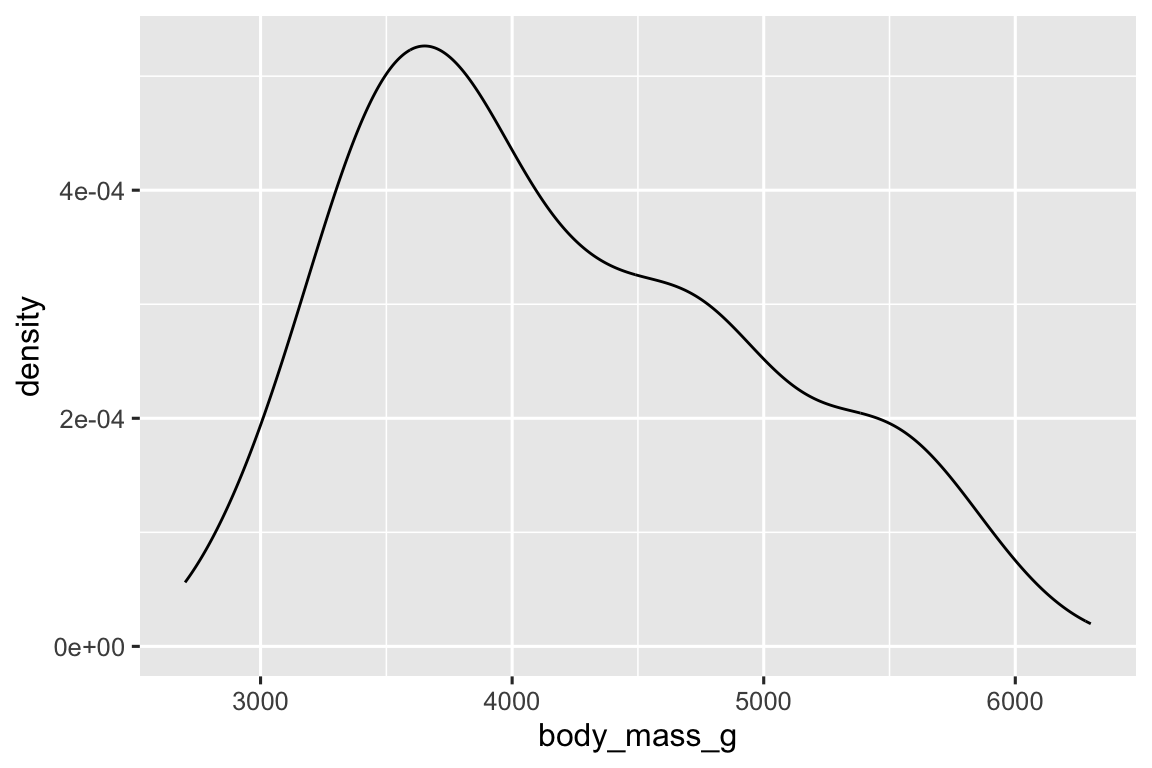

2.7.3 Exercises

1. Make a bar plot of species of penguins, where you assign species to the y aesthetic. How is this plot different?

2. How are the following two plots different? Which aesthetic, color or fill, is more useful for changing the color of bars?

   ggplot(penguins, aes(x = species)) +
     geom_bar(color = "red")
   
   ggplot(penguins, aes(x = species)) +
     geom_bar(fill = "red")

3. What does the bins argument in geom_histogram() do?

4. Make a histogram of the carat variable in the diamonds dataset that is available when you load the tidyverse package. Experiment with different binwidths. What binwidth reveals the most interesting patterns?

2.8 Visualizing relationships

To visualize a relationship we need to have at least two variables mapped to aesthetics of a plot. In the following sections you will learn about commonly used plots for visualizing relationships between two or more variables and the geoms used for creating them.

2.8.1 A numerical and a categorical variable

To visualize the relationship between a numerical and a categorical variable we can use side-by-side box plots. A boxplot is a type of visual shorthand for measures of position (percentiles) that describe a distribution. It is also useful for identifying potential outliers. As shown in Figure 2.1, each boxplot consists of:

• A box that indicates the range of the middle half of the data, a distance known as the interquartile range (IQR), stretching from the 25th percentile of the distribution to the 75th percentile. In the middle of the box is a line that displays the median, i.e. 50th percentile, of the distribution. These three lines give you a sense of the spread of the distribution and whether or not the distribution is symmetric about the median or skewed to one side.

• Visual points that display observations that fall more than 1.5 times the IQR from either edge of the box. These outlying points are unusual so are plotted individually.

• A line (or whisker) that extends from each end of the box and goes to the farthest non-outlier point in the distribution.

Figure 2.1: Diagram depicting how a boxplot is created.

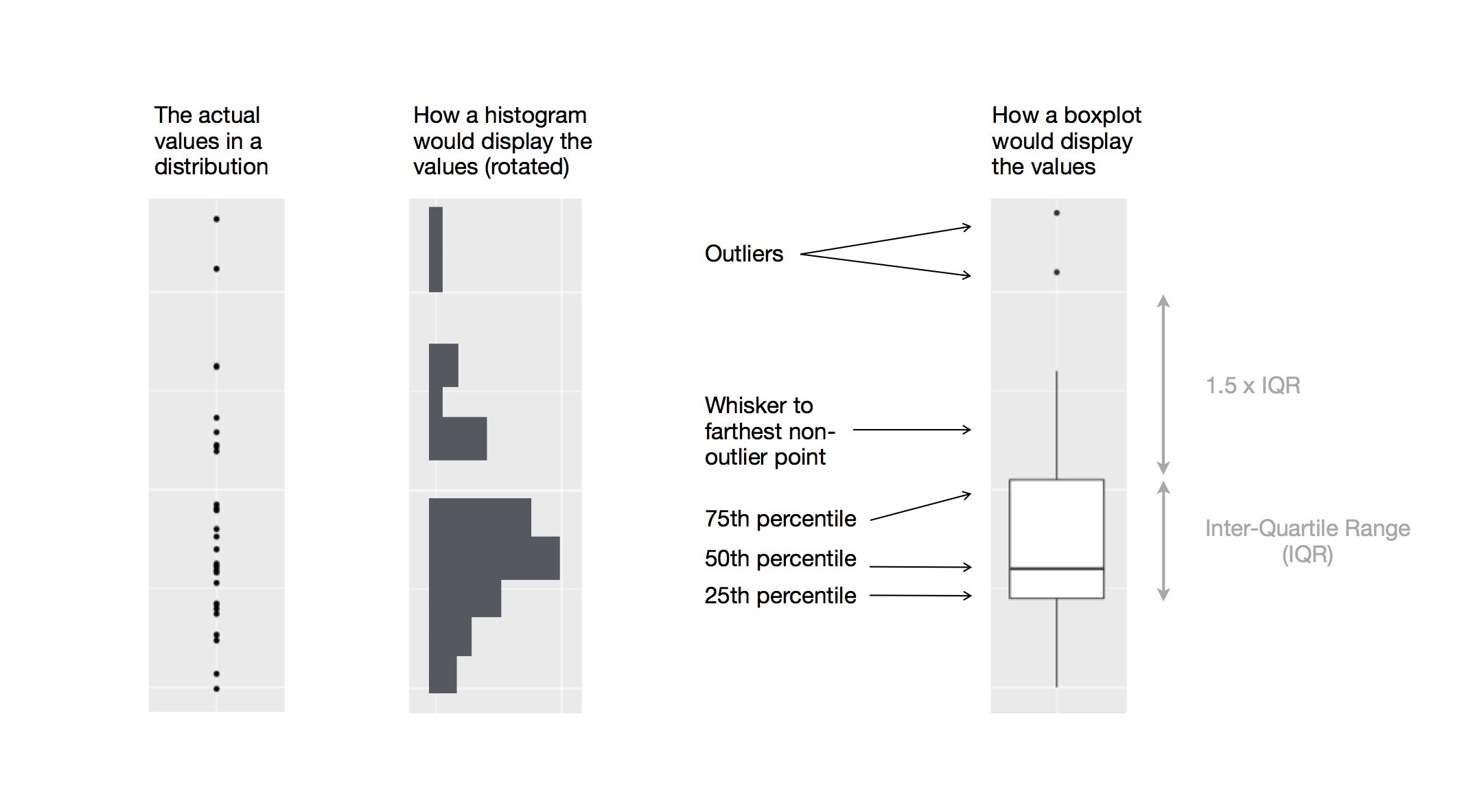
Let’s take a look at the distribution of body mass by species using geom_boxplot():

ggplot(penguins, aes(x = species, y = body_mass_g)) +
  geom_boxplot()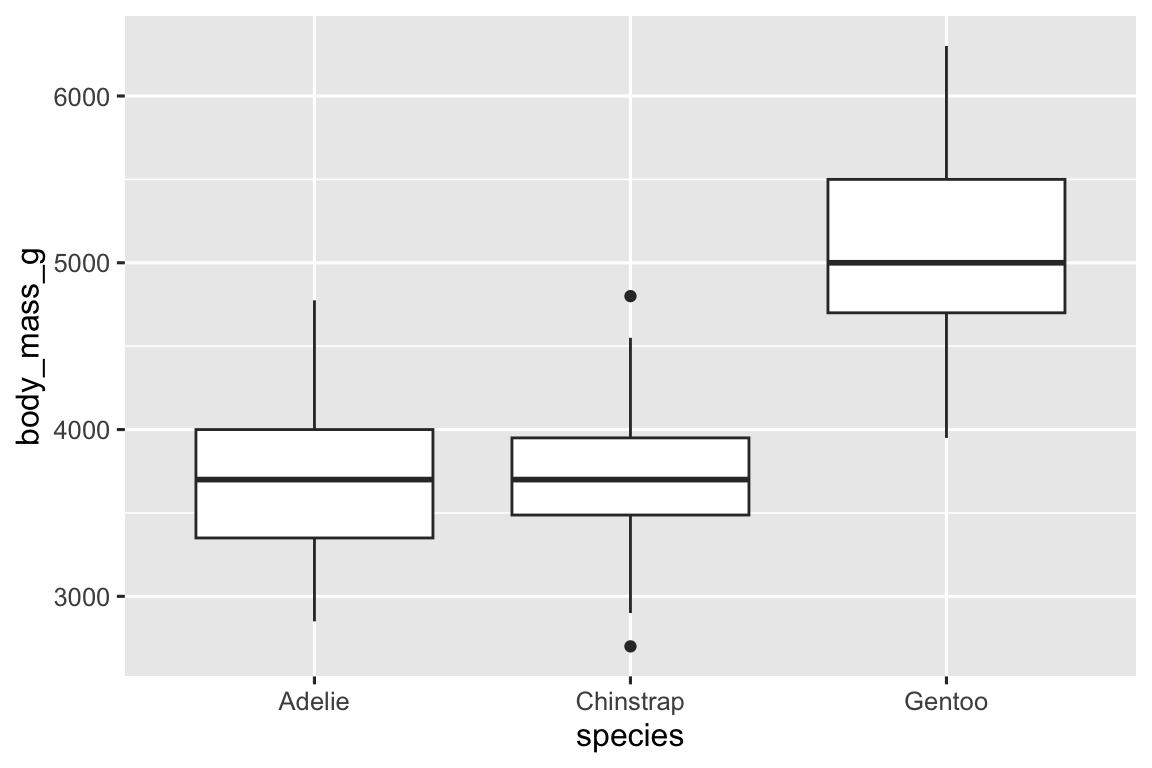

Alternatively, we can make density plots with geom_density().

ggplot(penguins, aes(x = body_mass_g, color = species)) +
  geom_density(linewidth = 0.75)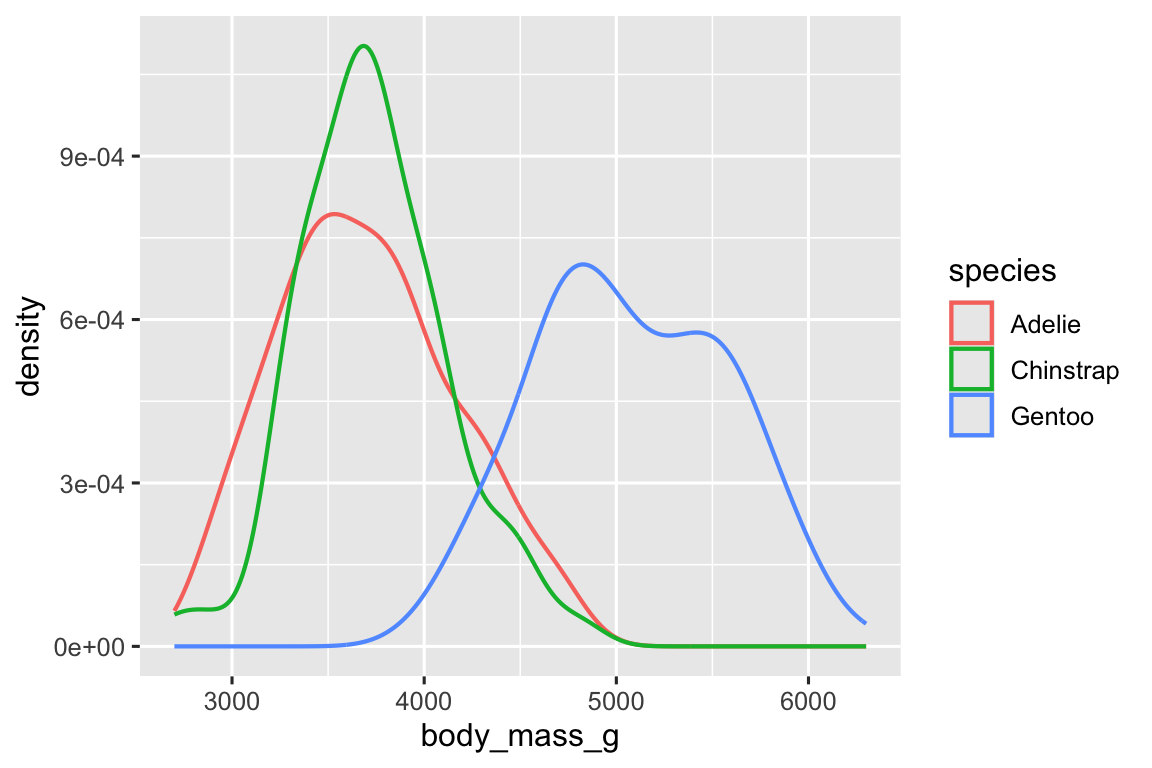

We’ve also customized the thickness of the lines using the linewidth argument in order to make them stand out a bit more against the background.

Additionally, we can map species to both color and fill aesthetics and use the alpha aesthetic to add transparency to the filled density curves. This aesthetic takes values between 0 (completely transparent) and 1 (completely opaque). In the following plot it’s set to 0.5.

ggplot(penguins, aes(x = body_mass_g, color = species, fill = species)) +
  geom_density(alpha = 0.5)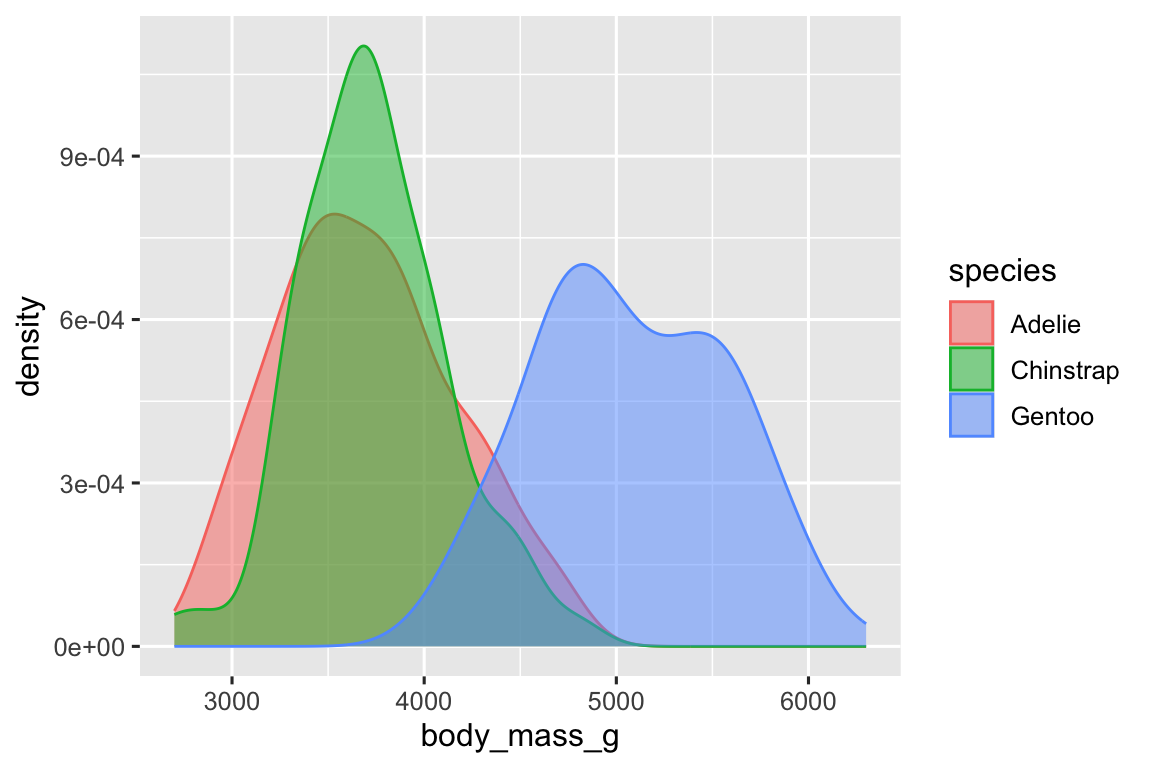

Note the terminology we have used here:

• We map variables to aesthetics if we want the visual attribute represented by that aesthetic to vary based on the values of that variable.
• Otherwise, we set the value of an aesthetic.

2.8.2 Two categorical variables

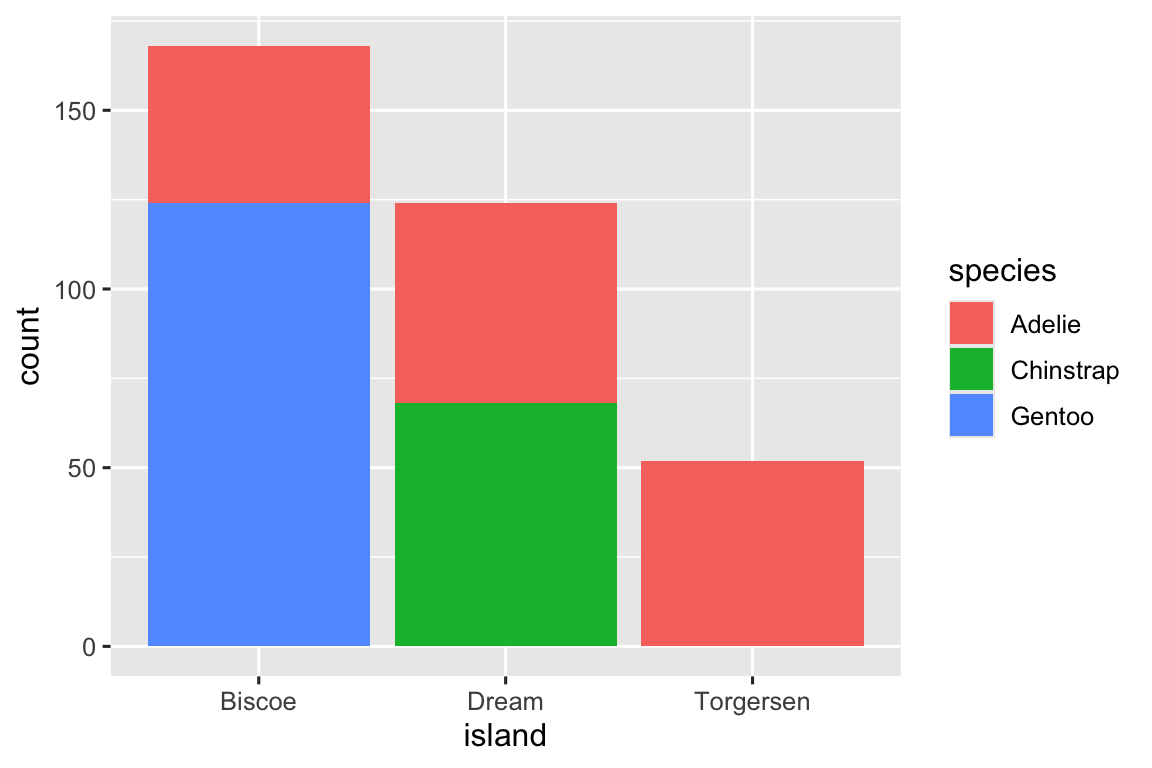
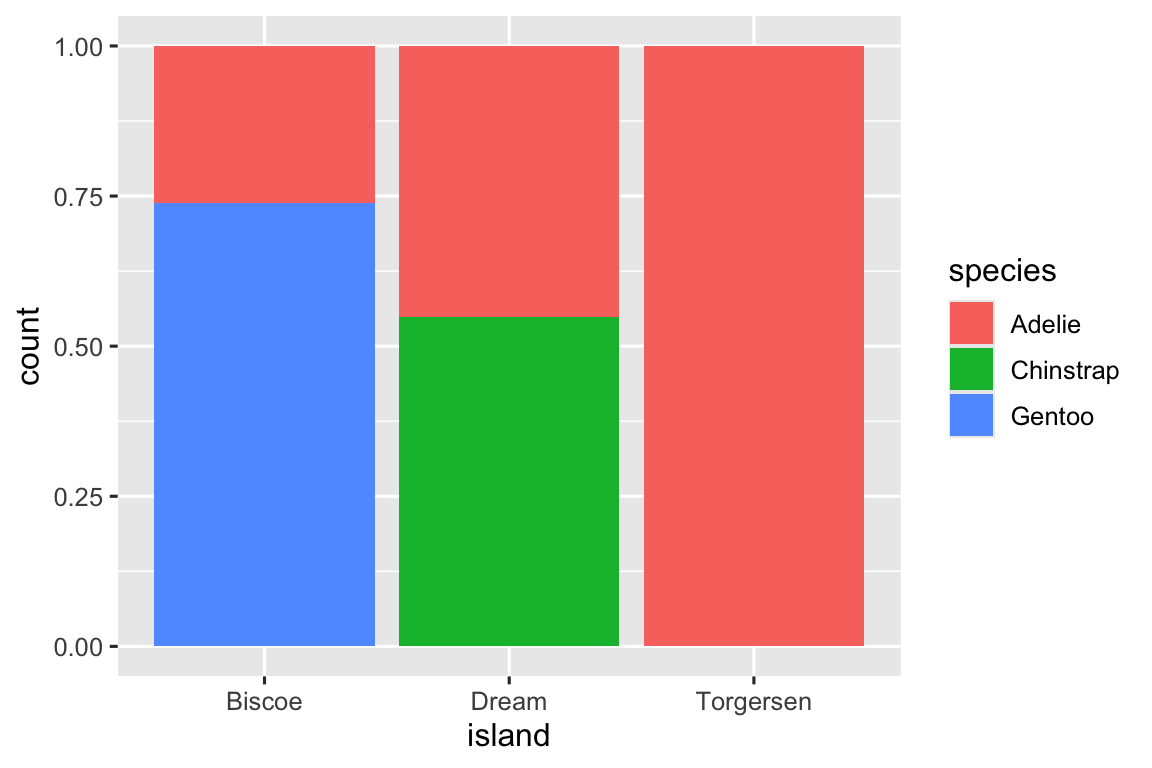
We can use stacked bar plots to visualize the relationship between two categorical variables. For example, the following two stacked bar plots both display the relationship between island and species, or specifically, visualizing the distribution of species within each island.

The first plot shows the frequencies of each species of penguins on each island. The plot of frequencies shows that there are equal numbers of Adelies on each island. But we don’t have a good sense of the percentage balance within each island.

ggplot(penguins, aes(x = island, fill = species)) +
  geom_bar()

The second plot, a relative frequency plot created by setting position = "fill" in the geom, is more useful for comparing species distributions across islands since it’s not affected by the unequal numbers of penguins across the islands. Using this plot we can see that Gentoo penguins all live on Biscoe island and make up roughly 75% of the penguins on that island, Chinstrap all live on Dream island and make up roughly 50% of the penguins on that island, and Adelie live on all three islands and make up all of the penguins on Torgersen.

ggplot(penguins, aes(x = island, fill = species)) +
  geom_bar(position = "fill")

In creating these bar charts, we map the variable that will be separated into bars to the x aesthetic, and the variable that will change the colors inside the bars to the fill aesthetic.

2.8.3 Two numerical variables

So far you’ve learned about scatterplots (created with geom_point()) and smooth curves (created with geom_smooth()) for visualizing the relationship between two numerical variables. A scatterplot is probably the most commonly used plot for visualizing the relationship between two numerical variables.

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point()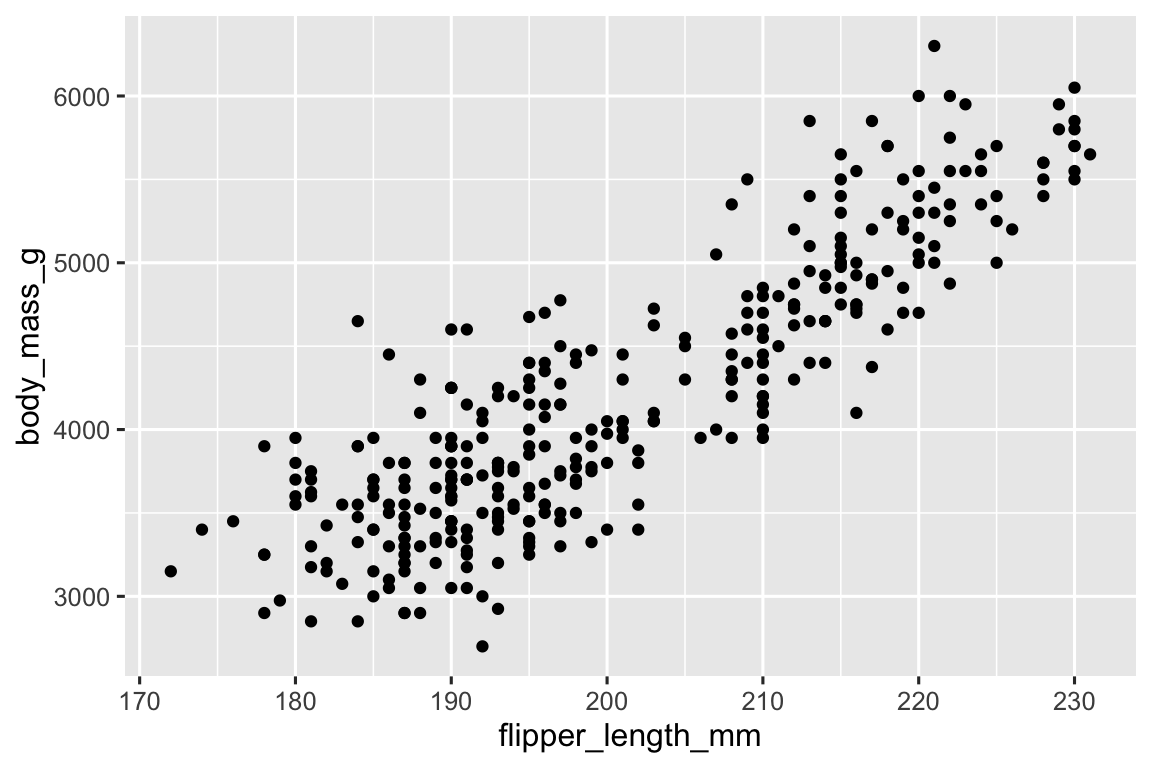

2.8.4 Three or more variables

As we saw in Section 2.3.6, we can incorporate more variables into a plot by mapping them to additional aesthetics. For example, in the following scatterplot the colors of points represent species and the shapes of points represent islands.

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point(aes(color = species, shape = island)) +
  scale_color_colorblind()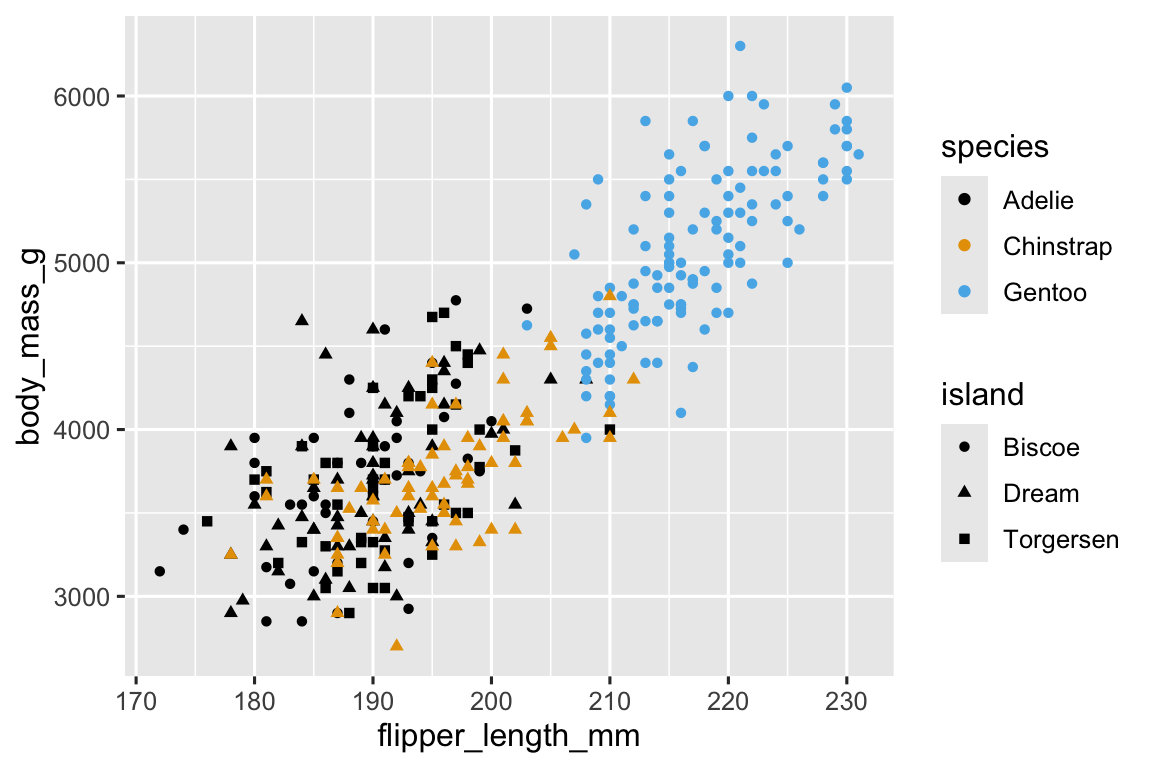

However adding too many aesthetic mappings to a plot makes it cluttered and difficult to make sense of. Another way, which is particularly useful for categorical variables, is to split your plot into facets, subplots that each display one subset of the data.

To facet your plot by a single variable, use facet_wrap(). The first argument of facet_wrap() is a formula¹, which you create with ~ followed by a variable name. The variable that you pass to facet_wrap() should be categorical.

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point(aes(color = species, shape = species)) +
  facet_wrap(~island) +
  scale_color_colorblind()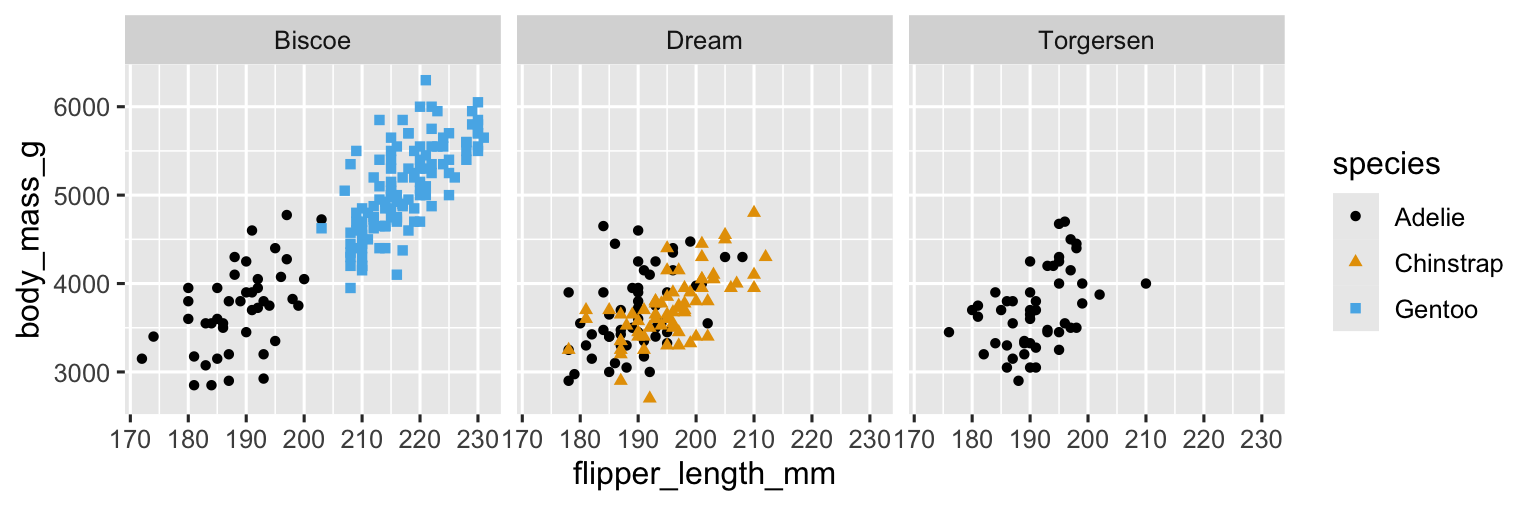

You will learn about many other geoms for visualizing distributions of variables and relationships between them in ?sec-layers.

2.8.5 Exercises

1. The mpg data frame that is bundled with the ggplot2 package contains 234 observations collected by the US Environmental Protection Agency on 38 car models. Which variables in mpg are categorical? Which variables are numerical? (Hint: Type ?mpg to read the documentation for the dataset.) How can you see this information when you run mpg?

2. Make a scatterplot of hwy vs. displ using the mpg data frame. Next, map a third, numerical variable to color, then size, then both color and size, then shape. How do these aesthetics behave differently for categorical vs. numerical variables?

3. In the scatterplot of hwy vs. displ, what happens if you map a third variable to linewidth?

4. What happens if you map the same variable to multiple aesthetics?

5. Make a scatterplot of bill_depth_mm vs. bill_length_mm and color the points by species. What does adding coloring by species reveal about the relationship between these two variables? What about faceting by species?

6. Why does the following yield two separate legends? How would you fix it to combine the two legends?

   ggplot(
     data = penguins,
     mapping = aes(
       x = bill_length_mm, y = bill_depth_mm, 
       color = species, shape = species
     )
   ) +
     geom_point() +
     labs(color = "Species")

7. Create the two following stacked bar plots. Which question can you answer with the first one? Which question can you answer with the second one?

   ggplot(penguins, aes(x = island, fill = species)) +
     geom_bar(position = "fill")
   ggplot(penguins, aes(x = species, fill = island)) +
     geom_bar(position = "fill")

2.9 Saving your plots

Once you’ve made a plot, you might want to get it out of R by saving it as an image that you can use elsewhere. That’s the job of ggsave(), which will save the plot most recently created to disk:

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point()
ggsave(filename = "penguin-plot.png")

This will save your plot to your working directory, a concept you’ll learn more about in ?sec-workflow-scripts-projects.

If you don’t specify the width and height they will be taken from the dimensions of the current plotting device. For reproducible code, you’ll want to specify them. You can learn more about ggsave() in the documentation.

Generally, however, we recommend that you assemble your final reports using Quarto, a reproducible authoring system that allows you to interleave your code and your prose and automatically include your plots in your write-ups. You will learn more about Quarto in ?sec-quarto.

2.9.1 Exercises

1. Run the following lines of code. Which of the two plots is saved as mpg-plot.png? Why?

   ggplot(mpg, aes(x = class)) +
     geom_bar()
   ggplot(mpg, aes(x = cty, y = hwy)) +
     geom_point()
   ggsave("mpg-plot.png")

2. What do you need to change in the code above to save the plot as a PDF instead of a PNG? How could you find out what types of image files would work in ggsave()?

2.10 Common problems 重要！常见问题

As you start to run R code, you’re likely to run into problems. Don’t worry — it happens to everyone. We have all been writing R code for years, but every day we still write code that doesn’t work on the first try!

Start by carefully comparing the code that you’re running to the code in the book. R is extremely picky, and a misplaced character can make all the difference. Make sure that every ( is matched with a ) and every " is paired with another ".

Sometimes you’ll run the code and nothing happens. Check the left-hand of your console: if it’s a +, it means that R doesn’t think you’ve typed a complete expression and it’s waiting for you to finish it. In this case, it’s usually easy to start from scratch again by pressing ESCAPE to abort processing the current command.

注意！

One common problem when creating ggplot2 graphics is to put the + in the wrong place: it has to come at the end of the line, not the start. In other words, make sure you haven’t accidentally written code like this:

ggplot(data = mpg) 
+ geom_point(mapping = aes(x = displ, y = hwy))

If you’re still stuck, try the help. You can get help about any R function by running ?function_name in the console, or highlighting the function name and pressing F1 in RStudio. Don’t worry if the help doesn’t seem that helpful - instead skip down to the examples and look for code that matches what you’re trying to do.

If that doesn’t help, carefully read the error message. Sometimes the answer will be buried there! But when you’re new to R, even if the answer is in the error message, you might not yet know how to understand it. Another great tool is Google: try googling the error message, as it’s likely someone else has had the same problem, and has gotten help online.

2.11 Summary 总结

In this chapter, you’ve learned the basics of data visualization with ggplot2. We started with the basic idea that underpins ggplot2: a visualization is a mapping from variables in your data to aesthetic properties like position, color, size and shape. You then learned about increasing the complexity and improving the presentation of your plots layer-by-layer. You also learned about commonly used plots for visualizing the distribution of a single variable as well as for visualizing relationships between two or more variables, by leveraging additional aesthetic mappings and/or splitting your plot into small multiples using faceting.

We’ll use visualizations again and again throughout this book, introducing new techniques as we need them as well as do a deeper dive into creating visualizations with ggplot2 in ?sec-layers through ?sec-communication.

With the basics of visualization under your belt, in the next chapter we’re going to switch gears a little and give you some practical workflow advice. We intersperse workflow advice with data science tools throughout this part of the book because it’ll help you stay organized as you write increasing amounts of R code.

---

1. Here “formula” is the name of the thing created by ~, not a synonym for “equation”.